Models¶
By design, the specification of models is done in its own namespace: model.
All model classes are subclasses of model.model. In the following
sections, I detail what each model can be used for and the mathematics behind
it.
SNooPy now has two different parametrizations for the shape of the
light-curves. One is the traditional 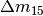 of
[Phillips 1999]_ and the newer ‘color-stretch’ introduced in
[Burns+2011], which more consistently deals with fast-declining events. Note
that the
of
[Phillips 1999]_ and the newer ‘color-stretch’ introduced in
[Burns+2011], which more consistently deals with fast-declining events. Note
that the EBV_model will only work with 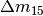 -based
templates.
-based
templates.
EBV_model¶
This light-curve model is a variation of that given by [Prieto+2006]. It
is most useful for determining a distance using the Phillips relation
and correcting for dust extinction in the host.
We compare the observed data in  filters to the following model:
filters to the following model:
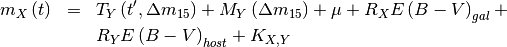
where 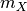 is the observed magnitude in band
is the observed magnitude in band 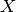 ,
, 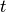 is the observed time relative to B maximum,
is the observed time relative to B maximum, 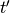 is the
de-redshifted time relative to B maximum,
is the
de-redshifted time relative to B maximum, 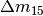 is the decline
rate parameter [Phillips1999],
is the decline
rate parameter [Phillips1999], 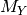 is the absolute
magnitude in filter
is the absolute
magnitude in filter 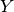 in the rest-frame of the supernova,
in the rest-frame of the supernova,
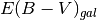 and
and 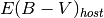 are the reddening due to
galactic foreground and host galaxy, respectively,
are the reddening due to
galactic foreground and host galaxy, respectively, 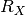 and
and
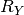 are the total-to-selective absorptions for filters
are the total-to-selective absorptions for filters 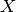 and
and
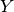 , respectively,
, respectively, 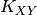 is the cross-band k-correction from
rest-frame
is the cross-band k-correction from
rest-frame 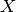 to observed filter
to observed filter 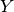 . Note that the k-corrections
depend on the epoch and can depend on the host and galaxy extinction (as
these modify the shape of the spectral template). In the fitting, one has the
choice of the spectral template of [Nugent+2002] or [Hsiao+2007]. The latter
is the default. You can choose to allow the K-corrections to vary during the
fit, keep them fixed, or not use them at all. See the parameters for the
. Note that the k-corrections
depend on the epoch and can depend on the host and galaxy extinction (as
these modify the shape of the spectral template). In the fitting, one has the
choice of the spectral template of [Nugent+2002] or [Hsiao+2007]. The latter
is the default. You can choose to allow the K-corrections to vary during the
fit, keep them fixed, or not use them at all. See the parameters for the
fit() function.
The template 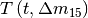 can be generated from
the code of citet{2006ApJ...647..501P} or citet{Burns2011}. In
the former case, you will be fitting to rest-frame
can be generated from
the code of citet{2006ApJ...647..501P} or citet{Burns2011}. In
the former case, you will be fitting to rest-frame 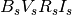 [1] while in the latter case, you can fit to
[1] while in the latter case, you can fit to 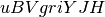 from the CSP
data [Contreras+2010]. You can mix and match which template
generator you use: it is all a matter of which filter you choose for
the
from the CSP
data [Contreras+2010]. You can mix and match which template
generator you use: it is all a matter of which filter you choose for
the restbands instance variable (see Doing the Fit).
In all, this model fits 4 parameters: Tmax, dm15,
EBVhost, and DM.
Note that to determine the host reddening, you need to fit at least
two distinct restframe filters. For now, I’ve left the galactic
and host reddening laws (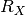 and
and 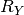 ) as member variables
rather than parameters to be fit
[2]. This could change in the future.
) as member variables
rather than parameters to be fit
[2]. This could change in the future.
EBV_model2¶
This is the same model as EBV_model, except that it can fit both
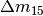 - and
- and  -based templates. And instead of the calibration
presented in [Folatelli+2010], the calibration from the
upcoming CSP analysis paper [Burns+2011] is used. When using
the
-based templates. And instead of the calibration
presented in [Folatelli+2010], the calibration from the
upcoming CSP analysis paper [Burns+2011] is used. When using
the choose_model function to select this model, you can
specify stype='dm15' or stype='st' to select the
two different light-curve parameters.
max_model¶
An alternative to assuming some kind of relationship between the different
filters (i.e., some kind of reddening law as is done in the EBV_model),
one can simply fit the maximum magnitude of each light-curve. This
is how the max_model model works. It uses the same light-curve
templates as EBV_model, but instead fits the following model:
![\[
m_{X}\left(t\right) = T_{Y}\left(t^\prime,\Delta m_{15}\right)+m_{Y}+R_{X}E\left(B-V\right)_{gal}+K_{X,Y}
\]](_images/math/174162d43f7e9a3b421127b3917e48ccc0dbc3ad.png)
where 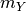 , the peak magnitude in filter
, the peak magnitude in filter 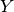 is now a parameter.
Of course, depending on the number of filters you fit, you will have
that many
is now a parameter.
Of course, depending on the number of filters you fit, you will have
that many 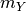 parameters. Note that K-corrections and Milky-way
extinction are performed exactly as in the
parameters. Note that K-corrections and Milky-way
extinction are performed exactly as in the EBV_model case.
Therefore, for 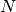 filters, max_model will have
filters, max_model will have 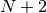 parameters:
parameters:
Tmax, dm15, and 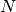 emph{f}``max``, where
emph{f} is the rest-band filter name (so if, for instance, you fit
an observed light-curve to restframe
emph{f}``max``, where
emph{f} is the rest-band filter name (so if, for instance, you fit
an observed light-curve to restframe 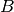 , there will be a
, there will be a Bmax
parameter). As with the EBV_model2 model, you can choose
which light-curve parameter you wish to use by specifying the stype
argument to choose_model().
NOTE: Please be aware that any non-linear fitter will only
find a emph{local} minimum in 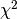 . It is up to you, the user,
to try different starting points in parameter space and see which
one gives the overall best-fit. After each fit, the member variable
. It is up to you, the user,
to try different starting points in parameter space and see which
one gives the overall best-fit. After each fit, the member variable
rchisq is updated with the reduced-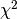 . You can therefore
use this to discriminate between different solutions.
. You can therefore
use this to discriminate between different solutions.
color_model¶
In this model, intrinsic colors from [Burns+2014] are used to
infer the amout of extinction 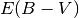 as well as the shape reddening
law
as well as the shape reddening
law 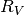 . Mathematically, the model being fit to the light-curves
is:
. Mathematically, the model being fit to the light-curves
is:
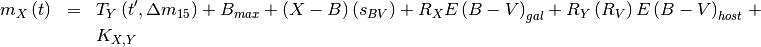
where 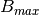 is the de-reddened and K-corrected
is the de-reddened and K-corrected 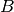 maximum (treated
as a free parameter) and
maximum (treated
as a free parameter) and 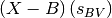 is the intrinsic
is the intrinsic
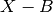 color, which is a function of
color, which is a function of  . In [Burns+2014]
it is modeled as a 2nd degree polynomial in
. In [Burns+2014]
it is modeled as a 2nd degree polynomial in 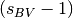 .
All other variables have the same meaning as in previous models. The
model has 5 free parameters:
.
All other variables have the same meaning as in previous models. The
model has 5 free parameters:  ,
, 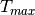 ,
, 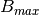 ,
, 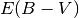 ,
and
,
and 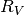 . Note that the distance modulus is not included in this
model.
. Note that the distance modulus is not included in this
model.
A major complication of this model is that two parameters, 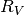 and
and 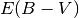 , appear as multiplicative factors in the same term.
At best, they will be highly covariant. At worst (for low values of
, appear as multiplicative factors in the same term.
At best, they will be highly covariant. At worst (for low values of
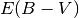 ), the model becomse insensitive to
), the model becomse insensitive to 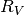 . For this reason,
it may be necessary to impose priors on
. For this reason,
it may be necessary to impose priors on 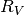 . Two such priors
were introduced in [Burns+2014]: a Gaussian mixture model that
applies to all SNeIa, and a binned prior, where a separate Gaussian
prior is applied to the SNIa depending on its value of
. Two such priors
were introduced in [Burns+2014]: a Gaussian mixture model that
applies to all SNeIa, and a binned prior, where a separate Gaussian
prior is applied to the SNIa depending on its value of 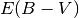 .
Because SNooPy uses the LM least-squares algorithm by default, there
is no natural way to incorporate these priors using the standard
.
Because SNooPy uses the LM least-squares algorithm by default, there
is no natural way to incorporate these priors using the standard fit()
routine. Instead, use the fitMCMC() routine, which fits the
light-curves using Markov Chain Monte Carlo and allows priors to be
specified on parameters. In this case, use the keyword argument rvprior='mix'
for the Gaussian mixture model, or rvprior='bin' for the
binned prior. See section Doing the Fit for more details.
| [Phillips1999] | Phillips, M.M., AJ, 118, 1766 (1999) http://adsabs.harvard.edu/abs/1999AJ....118.1766P |
| [Nugent+2002] | Nugent et al., PASP, 114, 803 (2002). http://adsabs.harvard.edu/abs/2002PASP..114..803N |
| [Hsiao+2007] | Hsiao et al., ApJ, 663, 1187 (2007). http://adsabs.harvard.edu/abs/2007ApJ...663.1187H |
| [Stritzinger+2005] | Stritzinger et al., PASP, 117, 810 (2005) http://adsabs.harvard.edu/abs/2005PASP..117..810S |
| [Contreras+2010] | Contreras et al., AJ, 139, 519 (2010). http://adsabs.harvard.edu/abs/2010AJ....139..519C |
| [Burns+2011] | (1, 2) Burns et al., AJ, 141, 19B (2011). http://adsabs.harvard.edu/abs/2011AJ....141...19B |
| [Burns+2014] | (1, 2, 3) Burns et al., ApJ, 789, 32B (2014). http://adsabs.harvard.edu/abs/2014ApJ...789...32B |
| [1] | The ‘s’ subscript refers to ‘standard’, which is to say the Bessel filters from [Stritzinger+2005] |
| [2] | So far, data I’ve analyzed hasn’t been good enough to distinguish between reddening laws. |