snpy package API¶

Module contents¶

SNPY 2.0 Author: Chris Burns (cburns@carnegiescience.edu)

SNPY (or SNooPy) is a Python package for fitting the light-curves of TypeIa supernovae. It is NOT an off-the-shelf program that will do all the work for you from the command line. It is meant to be run interactively. It provides many tools, but does not lock you into a specific routine for fitting and therefore allows for a great deal of customization. The package also contains a number of stand-alone sub-packages that can be installed seperately.

Documentation can be found the the doc/ directory under the source tree. But briefly, here is what SNOOPY can do:

Fit lightcurve templates to data. These templates were constructed from the Carnegie Supernova Project’s low-z data set (as outlined in Contreras et al. (2009) and Follatelli et al. (2009)). These include templates for the CSP uBVgriYJH filter set. You can also use Jose- Louis Prieto’s templates to fit Johnson/Kron/Cousins BRVI lightcurves.

Using templates, fit for distance (and dm15, E(B-V), stretch, time of maximum, etc. This uses the calibration of Follatelli et al. (2009) for the CSP filter set, or Prieto et al. (2006) for the BVRI set.

Alternatively, fit for light-curve parameters only (dm15, stretch, time of maximum, maximum light, colors, etc).

Compute k-corrections based on the spectral energy distribution template of Hsiao et al. (2007). This includes color-matching the SED template to the observed filters. You can do plain K-corrections or cross-band K-corrections.

Fit splines to light-curves to do your own analysis, independent of the light-curve templates.

Built-in Lira Law to estimate E(B-V).

Various plotting routines.

Interact with a properly set-up SQL database.

Subpackages¶

Submodules¶

snpy.sn module¶

class snpy.sn.dict_def(parent, dict={})¶: A class that acts like a dictionary, but if you ask for a key that is not in the dict, it returns the key instead of raising an exception.

snpy.sn.fix_arrays(node)¶: A recursive function that seeks out Numeric arrays and replaces them with numpy arrays.

snpy.sn.get_sn(str, sql=None, **kw)¶: Attempt to get a sn object from several possible sources. First, if str corresponds to an existing file name, the function attempts to load the sn instance from it as if it were a pickle’d object. If that fails, it attempts to use import_lc() on the file. If str is not the name of an existing file, it is treated as a SN name and is retrieved from the designated sql connection object (or default_sql if sql=None), in which case all keyword arguments are sent as options to the sql module.

snpy.sn.import_lc(file)¶: Import SN data from a datafile in the following format: line 1: name z ra decl line 2: filter {filter name} line 3: Date magnitude error ... line N: filter {filter name} line N+1: Date magnitue error ....

snpy.sn.save(instance, file)¶: Save a super instance to a file to be loaded back later with load().

class snpy.sn.sn(name, source=None, ra=None, dec=None, z=0)¶

Bases: object

This class is the heart of SNooPy. Create a supernova object by calling the constructor with the name of the superova as the argument. e.g:

In[1]:  s = sn('SN1999T')

if the supernova is in the SQL database, its lightcurve data will be loaded into its member data. Once the object is created, use its member data and functions to do your work. Of course, you can have multiple supernovae defined at the same time.

Parameters:	name (str) – A SN name, or a filename containing data. source (sqlbase) – An instance of sqlmod.sqlbase class (for database access) ra (float) – degrees Right-ascention (J2000), of object dec (float) – degrees Declination (J2000) of object z (float) – heliocentric redshift of object

__eq__(other)¶: Check if the data in this instance is equal to the data in another. Only checks raw data (light-curves).

bolometric(bands, method='direct', lam1=None, lam2=None, refband=None, EBVhost=None, Rv=None, redlaw=None, extrap_red='RJ', Tmax=None, interpolate=None, mopts={}, SED='H3', DM=None, cosmo='LambdaCDM', use_stretch=False, verbose=False, outfile=None, extra_output=False)¶

Produce a quasi-bolometric flux light-curve based on the input [bands] by integrating a template SED from lambda=lam1 to lambda=lam2.

Parameters:

bands (list) – list of filters to constrain the bolometric flux
method (str) – The method to use: ‘direct’ or ‘SED’. See SNooPy documentation for how these methods differ
lam1,lam2 (float) – limits of the integration. This is igored for the direct method.
refband (str or None) – For the SED method, the band to use to normalize the SED. If you have more confidence in one particular filter (or want to avoid automatically choosing a bad one), specify this. Ignored by the direct method.
EBVhost (float or None) – The value of E(B-V) to use for the host galaxy. If None, will look for model parameter in the supernova object.
Rv (float or None) – Value of R_V to use for the host galaxy. If None, will look for parameter in the supernova object.
redlaw (str) – The reddening law to use (‘ccm’,’fm’,’etc). If None, will look up in sn model.
extrap_red (str or None) – Specify how we extrapolate to lambda -> lam1 ‘RJ’ specifies Rayleigh-Jeans. None turns off extrapolation in the red.
Tmax (float or None) – Used by SED method to set the epoch of maximum. If None, will look for it as parameter in model.
interpolate (str or None) – if not None, missing photometry for each epoch will be interpolated. If ‘spline’, it will use a spline, if ‘model’, it will use the currently fit model.
mopts (dict) – You can pass any parameters for mangle_spectrum2() using this option. Only used by SED method.
SED (str, tuple, function) – Specify the SED to use. This can be a string (“H3”,”H”,”N”, or “91bg”), a (wave,flux) tuple, or a python function f(t) that, given time t, returns a (wave,flux) tuple. For the SED method, this is the SED that will be fluxed, then integrated. For the direct method, it is used to compute effective wavelenth of the filter and convert mag -> flux.
DM (float or None) – The distance modululs. If None, it will be computed using the supernova’s z_cmb and the specified cosmology (see cosmo argument below).
cosmo (string) – The cosmology to use. See astropy.cosmology.
use_stretch (bool) – If dm15 or stretch are defined, use this to de-stretch the SED template? Ignored by direct method.
verbose (bool) – Be verbose?
outfile (str) – If not None, name of output file for bolometric luminosities.
extra_output (bool) – If True, return a dictionary as extra element (see returns)

Returns:

(epoch, bolo, filters_used, limits): epoch: array of epochs bolo: array of bolometric luminosities in erg/s filters_used: a list of filters used for each epoch limits: 2-type of wavelength limits for each epoch
If extra_output is True, also return a dict as 4th element: containing the following keys: mflux: the mangled flux (or inferred flux) mfuncs: the mangling functions mwave: the wavelength vector or effective wavelenghts mags: the magnitudes to which we mangled the SED masks: th

Return type:

3 or 4-tuple

choose_model(name, stype='dm15', **kwargs)¶

A convenience function for selecting a model from the model module. [name] is the model to use. The model will be used when self.fit() is called and will contain all the parameters and errors. Refer to model for models and their parameters.

Parameters:	name (str) – The name of the model (default: `EBV_model`) stype (str) – the template parameter (`dm15` or `st`) kwargs (dict) – Any other arguments are sent to model’s constructor
Returns:	None

closest_band(band, tempbands=None, lowz=0.15)¶: Find the rest-frame filter in [tempbands] that is closest to the observed filter [band]. If tempbands is None, defaults to self.template_bands. In the case where the redshift of the SN is below [lowz], if [band] is in [tempbands], use [band] regardless of whether another band is closer.

compute_w(band1, band2, band3, R=None)¶

Returns the reddeining-free magnitude (AKA Wesenheit function) in the sense that: w = band1 - R(band1,band2,band3)*(band2 - band3) for for instance compute_w(V,B,V) would give: w = V - Rv(B-V)

Parameters:	band1,band2,band3 (str) – The three filters defining w R (float or None) – the R parameter to use (if None, compute assuming reddening due to dust with reddening law R_V = self.Rvhost

dump_lc(epoch=0, tmin=-10, tmax=70, k_correct=0, mw_correct=0)¶

Outputs several files that contain the lc information: the data, uncertainties, and the models themselves.

Parameters:	epoch (bool) – If True, output times relative to Tmax tmin/tmax (float) – the time range over which to output the model (default: -10 days to 70 days after Tmax) k_correct (bool) – If True, k-correct the data/models (default: False) mw_correct (bool) – If True, de-reddent the MW extintcion (default: False)
Returns:	None

Effects:

This function will create several files with the following template names:

{SN}_lc_{filter}_data.dat

{SN}_lc_{filter}_model.dat

which will contain the photometric data and model for each filter (if that filter was fit with a model). In the *_data.dat, there is an extra flag column that indicates if the k-corrections are valid (0) or invalid (1).

fit(bands=None, mangle=1, kcorr=1, reset_kcorrs=1, k_stretch=True, margs={}, **args)¶

Fit the N light curves with the currently set model (see self.choose_model()). The parameters that can be varried or held fixed depend on the model being used (try help(self.model) for this info). If one of these parameters is specified with a value as an argument, it is held fixed. Otherwise it is varied. If you set a parameter to None, it will be automoatically chosen by self.model.guess().

Parameters:

bands (list or None) – List of observed filters to fit. If None (default), fit all filters with valid rest-bands.
mangle (bool) – If True, mangle the Ia SED to fit observed colors before computing k-corrections.
kcorr (bool) – If True, compute k-corrections as part of the fit.
reset_kcorrs (bool) – If True, zero-out k-corrections before fitting.
k_stretch (bool) – If True, stretch the Ia SED in time to match dm15/st of the object.
margs (dict) – A set of extra arguments to send to kcorr.mangle_spectrum.mangle_spectrum2()
args (dict) – Any extra arguments are sent to the model instance If an argument matches a parameter of the model, that parameter will be held fixed at the specified value.

NOTE: If you have data that has already been k-corrected (either: outside SNooPy or by setting the individual data’s K attributes, use kcorr=0 and reset_kcorrs=1. If you have run the self.kcorr() manually and want to keep those k-corrections, use kcorr=0 and reset_kcorrs=0. Otherwise, use the default kcorr=1 and reset_kcorrs=1.

Returns:	None

Effects:: If successful, the model instance is updated with the best-fit values of the parameters. If self.replot is True, then a plot will be generated with the fit. self.ks will be filled in with k-corrections.

fitMCMC(bands=None, Nwalkers=None, threads=1, Niter=500, burn=200, tracefile=None, verbose=False, plot_triangle=False, **args)¶

Fit the N light curves of filters specified in [bands] with the currently set model (see self.choose_model()) using MCMC. Note that this function requires the emcee module to do the sampling. You should do an initial fit using the regular least-squares fit() function to compute good K-corrections and also get a starting point. The parameters that can be varried or held fixed depend on the model being used (try help(self.model) for this info). Parameters can be given priors by setting values to them as arguments (e.g., Tmax=0). This can be done in one of several ways:

specify a floating point number. The parameter is held fixed at that value.
specify a shorthand string:
- U,a,b: Uniform prior with lower/upper limits equal to a/b
- G,m,s: Gaussian prior with mean m and std dev. s.
- E,t: Exponential positive prior: p = exp(-x/tau)/tau x > 0
specify a function that takes a single argument: the value of the parameter and returns thei the prior as a log-probability.

Parameters:

bands (list or None) – a list of observed filters to fit. If None, all filters with valid rest-frame filters are fit.
Nwalkers (int or None) – Number of emcee walkers to spawn. see emcee documentation.
threads (int) – Number of threads to spawn. Usually not very useful as overhead requires more CPU than computing the model.
Niter (int) – Number of interations to run per walker.
burn (int) – burn-in iterations
tracefile (str) – Optional name of a file to which the traces of the MCMC will be stored.
verbose (bool) – be verbose?
plot_triangle (bool) – If True, plot a covariance plot. This requires the triangle_plot module (get it from pypi).
args (dict) – Any extra arguments are sent to the model instance’s fit() function. Note that if an argument matches a parameter name, it is treated specially as described above.

getEBVgal(calibration='SF11')¶

Gets the value of E(B-V) due to galactic extinction. The ra and decl member varialbles must be set beforehand.

Parameters:	calibration (str) – Which MW extionction calibraiton (‘SF11’ or ‘SFD98’)
Returns:	None

Effects:: self.EBVgal is set to Milky-Way color excess.

get_color(band1, band2, interp=1, use_model=0, model_float=0, kcorr=0)¶

return the observed SN color of [band1] - [band2].

Parameters:

band1,band2 (str) – Filters comprising the color
interp (bool) – If True, interpolate missing data in either filter
use_model (bool) – If True and both a model and interpolator are defined for the filter, use the model to interpolate
model_float (bool) – If True, then re-fit the model to each filter independently (so each has independent Tmax)
kcorr (bool) – If True, return k-corrected color.

Returns:

(MJD, color, error, flag)

MJD (float array):

epoch

color (float array):

observed color

error (float array):

uncertainty in color

flag (int array):

binary flag. Each of the following conditions are logically-or’ed:

0 - both bands measured at given epoch
1 - only one band measured
2 - extrapolation (based on template) needed, so reasonably safe
4 - interpolation invalid (extrapolation or what have you)
8 - One or both k-corrections invalid

Return type:

4-tuple

get_distmod(cosmo='LambdaCDM', **kwargs)¶

Gets the distance modulus based on a given cosmology. Requires the astropy module to work.

Parameters:	cosmo (str) – The cosmology to use. The available cosmologies are those in astropy.cosmology and kwargs can be set if the cosmology takes them (see astropy.cosmology) Default: LambdaCDM with Ho=74.3, O_m = 0.27, O_de = 0.73 kwargs (dict) – Extra arguments for given cosmology
Returns:	mu, the distance modulus in magnitudes.
Return type:	float

get_lb()¶

Computes the galactic coordinates of this objects.

Returns:	(l,b) l: galactic longitude (in degrees) b: galactic latitude (in degrees)
Return type:	2-tuple

get_mag_table(bands=None, dt=0.5, outfile=None)¶

This routine returns a table of the photometry, where the data from different filters are grouped according to day of observation. The desired filters can be specified, otherwise all filters are returned. When data is missing, a value of 99.9 is inserted.

Parameters:	bands (list) – filters to include in the table dt (flaot) – controls how to group by time: observations separated by less than `dt` in time are grouped. outfile (str or open file) – optinal file name for output
Returns:	numpy arrays keyed by: `MJD`: the epoch of observation [band]: the magnitude in filter [band] e_[band]: the error in [band]
Return type:	dict
Raises:	`TypeError` – the outfile is an incorrect type.

get_mangled_SED(band, i, normalize=True)¶

After the mangle_kcorr function has been run, you can use this function to retrieve the mangled SED that was used to compute the k-correction for the [i]’th day in [band]’s light-curve.

Parameters:

band (str) – the refernece filter
i (int) – index of filter [band]’s photometry
normalize (bool) – If True, normalize the SED to observed flux.

Returns:

(wave, mflux, oflux, mfunc)

wave: wavelength of SED in AA
mflux: mangled SED flux
oflux: original (un-mangled) SED flux
mfunc: mangling function evaluated at [wave]

Return type:

4-tuple

get_max(bands, restframe=0, deredden=0, use_model=0)¶

Get the maximum magnitude in [bands] based on the currently defined model or spline fits.

Parameters:	bands (list) – List of filters to fine maximum restframe (bool) – If True, apply k-corrections (default: False) deredden (bool) – If True, de-redden using Milky-Way color excess and any model color excess, if defined (default: False) use_model (bool) – If True and both a model and interpolator are defined for a filter, use the model. (default: False, i.e., use interpolator)
Returns:	(Tmax, Mmax, e_Mmax, rband) Tmax: array of time-of-maximum, one for each of [bands] Mamx: array of maximum magnitudes e_Mmax: error rband: list of rest-bands (if model was used to interpolate)
Return type:	4-tuple

get_restbands()¶

Automatically populates the restbands member data with one of the filters supported by the currently selected model. The filter with the closest effective wavelength to the observed filter is selected.

Returns:	none

Effects:: self.restbands is updated with valid filter set.

get_zcmb()¶: Gets the CMB redshift from NED calculator and stores it locally.

kcorr(bands=None, mbands=None, mangle=1, interp=1, use_model=0, min_filter_sep=400, use_stretch=1, **mopts)¶

Compute the k-corrections for the named filters. In order to get the best k-corrections possible, we warp the SNIa SED (defined by self.k_version) to match the observed photometry. Not all bands will be observed on the same day (or some data may be less than reliable), so there are several arguments that control how the warping is done.

Parameters:

bands (list or None) – List of filters to k-correct or all if None (default: None)
mbands (list of None) – List of filters to use for mangling the SED. (default: None: same as bands)
mangle (bool) – If True, mangle (color-match) the SED to observed colors. (default: True)
interp (bool) – If True, interpolate missing colors. (default: True)
use_model (bool) – If True, use a model to interpolate colors, if one exists (default: False)
min_filter_sep (float) – Filters whose effective wavelength are closer than this are rejected. (Default: 400 A)
use_stretch (bool) – If True, stretch the SED in time to match the stretch/dm15 of the object. (Default: True)
mopts (dict) – Any additional arguments are sent to the function mangle_spectrum.mangle_spectrum2()

Returns:

None

Effects:

Upon successful completion, the following member variables will be populated:

self.ks: dictionary (indexed by filter) of k-corrections
self.ks_mask: dictionary indicating valid k-corrections
self.ks_tck: dictionary of spline coefficients for the k-corrections

(useful for interpolating the k-corrections).
self.mopts: If mangling was used, contains the parameters of the

mangling function.

lc_offsets(min_off=0.5)¶

Find offsets such that the lcs, when plotted, won’t overlap.

Parameters:	min_off (float) – the minimum offset between the light-curves.
Returns:	list of offsets, in the order in which filters are plotted (controled by self.filter_order)
Return type:	list

lira(Bband, Vband, interpolate=0, tmin=30, tmax=90, plot=0, kcorr=1)¶

Use the Lira Law to derive a color excess. [Bband] and [Vband] should be whichever observed bands corresponds to restframe B and V, respectively. The color excess is estimated to be the median of the offset between the Lira line and the data. The uncertainty is 1.49 times the median absolute deviation of the offset data from the Lira line.

Parameters:

Bband (str) – the observed filter corresponding to B-band
Vband (str) – the observed filter corresponding to V-band
interpolate (bool) – If true and a model (or interpolator) exists for the observed filters, use it to interpolate missing B or V data
tmin/tmax (flaot) – range over which to fit Lira Law
plot (bool) – If True, produce a plot with the fit.
kcoor (bool) – If True, k-correct the data before fitting

Returns:

(EBV, error, slope)

EBV: the E(B-V) color-excess error: undertainty based on fit slope: the late-time slope of the B-V color curve

Return type:

3-tuple

mask_SNR(minSNR)¶

Mask out data with signal-to-noise less than [minSNR].

Parameters:	minSNR (float) – minimum signal-to-noise ratio needed for good data.
Returns:	None

Effects:: the mask attribute for every lc instance in self.data is udpated.

mask_data()¶: Interactively mask out bad data and unmask the data as well. The only two bindings are “A” (click): mask the data and “u” to unmask the data.

mask_emag(emax)¶

Mask out data with (magnitude) error larger than [emax].

Parameters:	emax (float) – maximum error allowed. All others masked out.
Returns:	None

Effects:: the mask attribute for every lc instance in self.data is udpated.

mask_epoch(tmin, tmax)¶

Mask out data in a time range (relative to B maximum) for all filters.

Parameters:	tmax (tmin,) – Time range over which to mask (good) data.
Returns:	None

Effects:: the mask attribute for every lc instance in self.data is udpated.

plot(**kwargs)¶

Plot out the supernova data in a nice format. There are many options for controlling the output.

Parameters:

xrange (2-tuple) – specify the x (time) range to plot (xmin,xmax)
yrange (2-tuple) – specify the y (mag/flux) range to plot (ymin,ymax)
title (str) – optional title
single (bool) – If True, plot out as a single (rather than panelled) plot with each filter a separate data set.
offset (bool) – If True, offset the lightcurves (for single plots) by constant amount such that they don’t cross.
legend (bool) – If True and single=True, plot the legend.
fsize (float) – override the font size used to plot the graphs (default: 12)
linewidth (int) – override the line width (default: 1)
symbols (dict) – dictionary of symbols, indexed by filter name.
colors (dict) – dictionary of colors to use, indexed by band name.
relative (bool) – If True, plot only relative magnitudes (normalized to zero). Default: False
mask (bool) – If True, omit plotting masked data.
label_bad (bool) – If True, label the masked data with red x’s?
Nxticks (int) – maximum number of x-axis tick marks (default: MPL auto)
JDoffset (bool) – If true, compute a JD offset and put it in the x-axis label (useful if x-labels are crowded) default: False
flux (bool) – If True, plot in flux units
epoch (bool) – If True, plot time relative to Tmax
outfile (str) – optional file name to save the plot
plotmodel (bool) – if True and both a model and spline are present, plot the model instead of spline.

plot_color(f1, f2, epoch=True, deredden=True, outfile=None, clear=True)¶

Plot the color curve (color versus time) given by f1 and f2.

Parameters:	f1,f2 (str) – The two filters defining the color (f1-f2) epoch (bool) – If True, plot time relative to Tmax deredden (bool) – If True, remove Milky-Way foreground reddening. outpfile (str) – Optional name for graph output to file.
Returns:	the figure istance with the plot.
Return type:	matplotlib.figure

plot_filters(bands=None, day=0, outfile=None, fill=False)¶

Plot the filter functions over a typical SN Ia SED.

Parameters:	bands (list or None) – filters to plot or, if None, all observed filters. day (int) – Which epoch (t-tmax) to use for retrieving the Ia SED outfile (str) – optional filename for graph output. fill (bool) – If True, use matplotlib’s fill_between to fill in filter and SED curves. Useful to gauge overlap.
Returns:	the figure instance for the plot.
Return type:	matplotlib.figure

plot_kcorrs(colors=None, symbols=None, outfile=None)¶

Plot the derived k-corrections after they have been computed. Both mangled and un-mangled k-corrections will be plotted as lines and points, respectively. If mangling was used to do the k-corrections, clicking ‘m’ on a point will bring up another plot showing the original and mangled spectrum.

Parameters:	colors (dict or None) – specify colors to use by giving a dictionary keyed by filter name symbols (dict or None) – specfiy symbols to use by givein a dictionary keyed by filter name outfile (str) – optional file name for outputting the graph to disk.
Returns:	the figure instance of the plot.
Return type:	matplotlib.figure

read_sql(name)¶

Get the data from the SQL server for supernova.

Parameters:	name (str) – The name to retrieve from the SQL database
Returns:	-1 for failure
Return type:	int

Effects:: If successful, the SN objects is updated with data from the SQL database.

save(filename)¶

Save this SN instance to a pickle file, which can be loaded again using the get_sn() function.

Parameters:	filename (str) – output filename
Returns:	None

summary(out=<open file '<stdout>', mode 'w'>)¶

Get a quick summary of the data for this SN, along with fitted parameters (if such exist).

Parameters:	out (str or open file) – where to write the summary
Returns:	None

systematics(**args)¶

Report any systematic errors that may be present in the fit parameters.

Parameters:	args (dict) – All arguments are sent to the model.systmatics() function.
Returns:	a dictionary of systematic errors keyed by parameter name. It therefore depends on the model being used. Also see the specific model for any extra arguments. If None is returned as a value, no systematic has been estimated for it.
Return type:	dict

update_sql(attributes=None, dokcorr=1)¶

Updates the current information in the SQL database, creating a new SN if needed.

Parameters:	attributes (list or None) – attributes of the SN to update. If None, then all attributes are updated. dokcorr (bool) – If True, also update the k-corrections in the DB.
Returns:	None

Effects:: SQL database is updated.

snpy.lc module¶

class snpy.lc.lc(parent, band, MJD, mag, e_mag, restband=None, K=None, SNR=None)¶

This class contains the data representing a lightcurve. This means the time (in MJD), magnitudes, uncertainties, fluxes, etc. It is meant to be contained by the snpy.sn class, to make for somewhat more convenient access to the data.

Parameters:

parent (snpy.sn instance) – the parent objects to which the data belongs
band (str) – the passband the data was observed through
MJD (float array) – date of observation. Even though it’s called MJD, no assumptions are made for epoch zero-point.
mag (float array) – observations in magnitudes
e_mag (float array) – error of observations in magnitudes
restband (str) – If different than the observed passs band.
K (float array) – If specified, K-corrections will be stored with the magnitudes. Do this to k-correct the data indpendent of fitting.
SNR (float array) – optional signal-to-noise of the data, if different than 1.087/e_mag.

__eq__(other)¶: Check to see if another lc instance is equal to this one.

compute_lc_params(N=50)¶

Compute dm15, Tmax, Mmax, and covariances for the light-curve.

Parameters:	N (int) – the nubmer of Monte-Carlo iterations for computing errors in parameters.
Returns:	None

Effects:

The foloowing LC instance’s member variables are updated:

Tmax: time of primary maximum. None if such does not exist
e_Tmax: error in Tmax
dm15: The decline rate parameter, or None if not measurable
e_dm15: error in dm15
Mmax: the magnitude at maximum, or None if no maximum.
e_Mmax: the error in Mmax
cov_Tmax_dm15: covariance between Tmax and dm15
cov_Mmax_dm15: covariance between Mmax and dm15
cov_Tmax_Mmax: covariance between Tmax and Mmax

curve_fit(fitflux=0, do_sigma=1, Nboot=100, keep_boot=1, method='spline2', **args)¶

Make a spline template of the lightcurve. The name is a bit misleading as many interpolators are available. Once this is done, the light-curve can be interpolated and properties (Tmax, Mmax, etc) can be computed.

Parameters:

fitflux (bool) – If True, fit the flux instead of magnitudes
do_sigma (bool) – If True, perform MC iterations to estimate the errors in the interpolations.
Nboot (int) – Number of MC iterations to perform.
keep_boot (bool) – If True, keep the MC realizations for future use
method (str) – The interpolation method. Use list_types() to find out what is available.
args (dict) – all other arguments are sent to the constructor of the interpolator. See snpy.utils.fit1dcurve for documentation on this.

Returns:

None

Effects:: Upon successful completion of the routine, the following member variables will be populated: * Tmax, e_Tmax: time of maximum (and error if do_sigma=1) * Mmax, e_Mmax: peak magnitude * dm15, e_dm15: delta-m 15 * model_type: “spline” or “spline2” * tck: spline info

eval(times, t_tol=-1, epoch=0)¶

Interpolate (if required) the data to specific times. If there is a data point “close enough”, that value is used without interpolation. If epoch is nonzero, then times are interpreted relative to parent.Tmax

Parameters:	times (float array) – times at which to interpolate t_tol (float) – If a data point is less than t_tol away from requested time, the data will be returned. Use -1 to always interpolate. epoch (bool) – If True, `lc.parent.Tmax` is added to times
Returns:	(mag,mask) mag (float array): interpolated magnitudes mask (bool array): True if interpolation is valid
Return type:	2-tuple
Raises:	`AttributeError` – if an interpolator for the data has not been assigned

get_SNR()¶: Get the signal-to-noise ratio of the data. This can also be accessed through the SNR attribute.

get_covar(flux=1)¶

returns the error matrix in flux units (unless flux=0). If this was not setup by the user, the variance will be returned as a 1-D array.i

Parameters:	flux (bool) – If true, return in flux units, otherwise in mags.
Returns:	the square covariance error matrix.
Return type:	float array

get_e_flux()¶: Get the flux error of the observations. This can also be access through the e_flux attribute.

get_flux()¶: Get the flux of the observations. This can also be access through the flux attribute.

get_t()¶: Get the epoch of observations relative to parent.Tmax. This can also be accessed through the t attribute.

mask_SNR(minSNR)¶

Update the lc’s mask to only include data with SNR > min.

Parameters:	minSNR (float) – minimum signal-to-noise for good data
Returns:	None

Effects:: The mask attribute is updated.

mask_emag(emax)¶

Update the lc’s mask to only include data with e_mag < max.

Parameters:	emax (float) – maximum error for good data
Returns:	None

Effects:: The mask attribute is updated.

mask_epoch(tmin, tmax)¶

Update the lc’s mask to only include data between tmin and tmax.i

Parameters:	tmin,tmax (float) – range over which data is considered good.
Returns:	None

Effects:: The mask attribute is updated.

plot(epoch=1, flux=0, gloes=True, symbol=4, outfile=None, use_model=True)¶

Plot this light-curve, including residuals if a model or interpolator is defined.

Parameters:

epoch (Bool) – If True, plot times relative to self.Tmax
flux (Bool) – If True, plot in flux units rather than magnitudes
gloes (Bool) – If True, use GLoEs to smooth data and produce model
symbol (misc) – Specify matplotlib symbol to use for plotting points
outfile (string or None) – If not None, output graph to specified file
use_model (Bool) – If True and both model and interpolator are defined, use the model to plot residuals.

Returns:

PanelPlot or SimplePlot instance. A reference to the plot instance created to show the data.

replot()¶: Replot a figure, if it exists and belongs to this instance.

spline_fit(fitflux=0, do_sigma=1, Nboot=100, keep_boot=1, method='spline2', **args)¶

Make a spline template of the lightcurve. The name is a bit misleading as many interpolators are available. Once this is done, the light-curve can be interpolated and properties (Tmax, Mmax, etc) can be computed.

Parameters:

fitflux (bool) – If True, fit the flux instead of magnitudes
do_sigma (bool) – If True, perform MC iterations to estimate the errors in the interpolations.
Nboot (int) – Number of MC iterations to perform.
keep_boot (bool) – If True, keep the MC realizations for future use
method (str) – The interpolation method. Use list_types() to find out what is available.
args (dict) – all other arguments are sent to the constructor of the interpolator. See snpy.utils.fit1dcurve for documentation on this.

Returns:

None

Effects:: Upon successful completion of the routine, the following member variables will be populated: * Tmax, e_Tmax: time of maximum (and error if do_sigma=1) * Mmax, e_Mmax: peak magnitude * dm15, e_dm15: delta-m 15 * model_type: “spline” or “spline2” * tck: spline info

template(fitflux=False, do_sigma=True, Nboot=50, method='gp', compute_params=True, interactive=False, **args)¶: A backwrd-compatibility alias for spline_fit().

snpy.model module¶

Model.py: a module that defines the SN models to be fit by SNOOPY.

A base class (Model) is defined to handle most of the heavy-lifting and boiler plate around scipy.optimize.leastsq. Defining a new model is done by sub- classing Model and overriding the member functions.

New: Add an optional [decline_param] to choose between a dm15 model and stretch: (st) model

class snpy.model.EBV_model(parent, stype='dm15')¶

Bases: snpy.model.model

This model fits any number of lightcurves with CSP uBVgriYJHK templates or Prieto BsVsRsIs templates. The parameters you can fit:

dm15 (decline rate)
Tmax (time of peak B maximum)
DM (distance modulus)
EBVhost (host galaxy extinction)

The model is constructed by assuming a peak B absolute magnitude and B-X colors based on the current value of dm15. The colors are from Folatelli et al. (2010), as are the calibration of Bmax vs dm15. For the latter, there are 6 calibrations, based on the sample used to make the fit. The default is 6 (best observed, excluding heavily extincted SNe), but you can choose a different calibration by setting that argument in the fit() call. Aside from the instrinsic colors, a global extinction parameter EBVhost is applied to each light-curve, as well as Milky way extinction from the SN object’s EBVgal. The value of R_V for the host galaxy is not a parameter, but is controled by the choice of calibration in order to remain consistent with Folatelli et al. (2009). The R_V for the galactic extinction is taken from the SN object (default 3.1).

MMax(band, calibration=6)¶: Given self.dm15, return the absolute magnitude at maximum for the given filter [band]. The calibration paramter allows you to choose which fit (1-6) in Folatelli et al. (2009), table 9

systematics(calibration=6, include_Ho=False)¶: Returns the systematic errors in the paramters as a dictionary. If no estimate is available, return None for that paramter.

class snpy.model.EBV_model2(parent, stype='st')¶

Bases: snpy.model.model

This model fits any number of lightcurves with CSP uBVgriYJHK templates or Prieto BsVsRsIs templates. The parameters you can fit:

dm15 or st (decline rate or stretch)
Tmax (time of peak B maximum)
DM (distance modulus)
EBVhost (host galaxy extinction)

The model is constructed by assuming a peak absolute magnitudes in tall the filters, as derived in Burns et al. 2011. Calibrations were determined using MCMC modeling on all filters at once, determining M_X and b_X for each filter, and one value for R_V. There are 2 calibrations, based on the sample used to make the fit and the prior used on the extinction. Default is 0, where the 2 red SNe are excluded and the blue sub-sample is used to anchor the colors. Value of 1 is for the sample where the two red SNe were included. A global extinction parameter EBVhost is applied to each light-curve, as well as Milky way extinction from the SN object’s EBVgal. The value of R_V for the host galaxy is not a parameter, but is controled by the choice of calibration R_V for the galactic extinction is taken from the SN object (default 3.1).

MMax(band, calibration=1)¶: Given self.dm15, return the absolute magnitude at maximum for the given filter [band]. The calibration paramter allows you to choose which fit (1-6) in Folatelli et al. (2009), table 9

systematics(calibration=1, include_Ho=False)¶: Returns the systematic errors in the paramters as a dictionary. If no estimate is available, return None for that paramter.

class snpy.model.Rv_model(parent, stype='dm15')¶

Bases: snpy.model.model

This model fits any number of lightcurves with CSP uBVgriYJHK templates or Prieto BsVsRsIs templates. The parameters you can fit:

dm15 (decline rate)
Tmax (time of peak B maximum)
Bmax (maximum B magnitude)
EBVhost (host galaxy extinction)
Rv (host galaxy reddening law)

The model is constructed by assuming a peak observed magnitude in B, value of dm15, and Tmax. This will fit the B-lightcurve. To fit the others, we use the Burns et al. (2011) calibrations to compute B - X intrinsic colors, add extinction consistent with the current value of Rv and EBVhost to get predicted maximum magnitudes.

MMax(band, calibration=1)¶: Given self.dm15, return the absolute magnitude at maximum for the given filter [band]. The calibration paramter allows you to choose which fit (1-6) in Folatelli et al. (2009), table 9

systematics(calibration=1, include_Ho=False)¶: Returns the systematic errors in the paramters as a dictionary. If no estimate is available, return None for that paramter.

class snpy.model.color_model(parent, stype='st', normfilter='B')¶

Bases: snpy.model.model

This model fits any number of lightcurves with CSP uBVgriYJHK templates or Prieto BsVsRsIs templates. The model is an observed B maximum (so B must be one of the restbands) and N-1 colors constructed from an intrinsic color-st/dm15 relation and extinction computed from E(B-V) and Rv. The parameters are:

st (decline rate)
Tmax (time of peak B maximum)
Bmax (maximum B magnitude)
EBVhost (host galaxy extinction)
Rv (host galaxy reddening law)

The assumed colors are take from Burns et al. (2014).

get_covar(band, t)¶: Return a covariance matrix to handle systematics

systematics(calibration=1, include_Ho=False)¶: Returns the systematic errors in the paramters as a dictionary. If no estimate is available, return None for that parameter.

class snpy.model.max_model(parent, stype='dm15')¶

Bases: snpy.model.model

This model is very similar to the EBV_model, but instead of having an extinction parameter (EBVhost) that controls all the colors, we simply fit a peak magnitude for each band independently. There are therefore a variable number of parameters, based on the number of bands you fit: - dm15 (decline rate parameter) - Tmax (time of maximum in B) - Xmax (peak magnitude in restband X). N of these for N bands. The lightcurves are constructed by offsetting each template by Xmax vertically and Tmax horizontally, as a function of dm15. Each band is also offset by R_X*EBVgal, where EBVgal is taken from the parent SN object (as is the value of R_V).

setup()¶: Since we have a variable number of parameters, we need to do this dynamically before the fitting is done.

class snpy.model.max_model2(parent, stype='dm15')¶

Bases: snpy.model.model

Same as max_model, but here we let Tmax for each filter be a free parameter.

setup()¶: Since we have a variable number of parameters, we need to do this dynamically before the fitting is done.

class snpy.model.model(parent)¶

The base class for SNooPy light-curve models. It contains the parameters to be solved and its __call__ function returns the model for a filter’s data. It has several convenience member functions for figuring out things like K-corrections and reddening coefficients.

MWR(band, t)¶

Determine the best 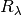$R_\lambda$ for the foreground MW extinction.

Parameters:	band (str) – The name of the filter t (float array) – The epoch (t - T(Bmax)) of the observations.
Returns:	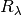$R_\lambda$ for the filter at times t.
Return type:	float array

fit(bands, epsfcn=0, **args)¶

Fit the model with currently fixed and free parameters againts the set of bands [bands]. All other arguments are passed directly to the model() member function as optional arguments. After running, the free parameters will be set to their fit values and self.C will contain the covariance matrix.

Parameters:	bands (list of str) – The filters to fit epsfcn (float) – see scipy.optmize.leastsq.
Returns:	None

Effects:: The member variables self.parameters and self.eparameters will be set with best-fit values. self.C will be updated with the values from the covariance matrix.

get_max(bands, restframe=0, deredden=0)¶

Get the maxima of the light-curves, given the current state of the model.

Parameters:

bands (list of str) – list of filters to find maxima for
restframe (bool) – If True, apply K-corrections to maximum magnitudes
deredden (bool) – If True, apply all known extinction corrections to maximum magnitudes. Note: this will always correct for Milky-Way extinction, but in some models, host-galaxy extinction may be removed as well.

Returns:

(Tmax,Mmax,eMmax,restbands):

Tmax (list of floats): Time of maxima for each filter
Mmax (list of floats): Maximum magnitudes for each filter
eMmax (list of floats): errors in maximum magnitudes
restbands (list of str): The rest-bands used to fit each observed

filter

Return type:

4-tuple

guess(param)¶

A function that is run and picks initial guesses for the parameter.

Parameters:	param (str) – the name of the parameter.
Returns:	initial guess for the parameter.
Return type:	Value

kcorr(band, t)¶

Convenience function to call back to the parent and get the k-corrections.

Parameters:

band (str) – the name of the filter
t (float array) – The epochs (t - T(Bmax)) of the observations

Returns:

2-tuple (K,mask)

K (float array): K-corrections
mask (bool array): True where K-corrections are valid

prior(param, value)¶

An optional prior on the parameters. To be filled in based on implementation. This should return the probability given the current value of a parameter.

Parameters:	param (str) – The name of the parameter value (float) – The current value of the parameter.
Returns:	prior – the probability of parameter.
Return type:	float

setup()¶: A function that does any initial setup (estimating k-correcions, etc)

systematics()¶

compute the systematic errors associated with the model paramters.

Parameters:	None –
Returns:	a dictionary of systematic errors keyed by parameter name. It therefore depends on the model being used. Also see the specific model for any extra arguments. If None is returned as a value, no systematic has been estimated for it.
Return type:	dict

snpy.kcorr module¶

A module for computing k-corrections. This code has been assembled from many sources, mostly from IRAF scripts written by Mark Phillips and IDL code written by Mark Sullivan.

Most of the heavy lifting w.r.t. integration of filters over the SED has been moved to the snpy.filter module.

snpy.kcorr.K(wave, spec, f1, f2, z, photons=1)¶

compute single K-correction based on a single spectrum and set of observed and rest-frame filters.

Parameters:

wave (float array) – input wavelength in Angstroms
flux (float array) – arbitrarily scaled flux
f1 (filter instance) – Rest-frame filter.
f2 (filter instance) – Observed filter. This could be the same as f1 or a redder filter for cross-band K-correction
z (float) – redshift
photons (bool) – If True, fluxes are computed in units of photons rather than energy (see Nugent+2002)

Returns:

(K,flag)

K: K-correction
flag: 1 -> success, 0->failed

Return type:

2-tuple

snpy.kcorr.R_obs(filter, z, days, EBVhost, EBVgal, Rv_host=3.1, Rv_gal=3.1, version='H', redlaw='f99', strict_ccm=False)¶: Compute the ‘true’ value of R based on a fiducial value of Rv for both Galactic and host extinction and the SED of a supernova. The filter is such that:

A(filter) = R(filter)*E(B-V).

snpy.kcorr.R_obs_abc(filter1, filter2, filter3, z, days, EBVhost, EBVgal, Rv_host=3.1, Rv_gal=3.1, version='H', redlaw='f99', strict_ccm=False)¶

Compute the observed value of the selective-to-total extinction, R, by applying an extinction curve to a set of library Ia spectral SEDs and computing synthetic photometry:

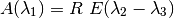
$A(\lambda_1) = R\ E(\lambda_2-\lambda_3)$

where

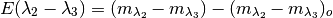
$E(\lambda_2-\lambda_3) = (m_{\lambda_2} - m_{\lambda_3}) - (m_{\lambda_2} - m_{\lambda_3})_o$

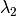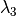ie, the color excess for filters $\lambda_2$ and $\lambda_3$ .

Parameters:

filter1,filter2,filter3 (str) – the 3 filters defining R
z (float) – redshift of host compoenent of extinction
days (int array) – epochs at which to comptue R (t-Tmax(B))
EBVhost (float) – host component of extinction to apply
EBVgal (float) – Milky-way (foreground) component of extinction to apply
Rv_host (float) – R_V for host component
Rv_gal (float) – R_V for MW component
version (str) – Version of Ia SED library. See get_SED().
redlaw (str) – Which reddening law to use. See snpy.utils.deredden
strict_ccm (bool) – If True and using CCM reddening law, do not apply the corrections due to O’Donnel.

snpy.kcorr.R_obs_spectrum(filts, wave, flux, z, EBVgal, EBVhost, Rv_gal=3.1, Rv_host=3.1, redlaw='f99', strict_ccm=False)¶: Compute the ‘true’ value of R based on a fiducial value of Rv for both Galactic and host extinction and the SED given by wave,flux for each filter in filters. The filter is such that: A(filter) = R(filter)*E(B-V).

snpy.kcorr.get_SED(day, version='H3', interpolate=True, extrapolate=False)¶

Retrieve the SED for a SN for a particular epoch.

Parameters:

day (int or float) – The integer day w.r.t. time of B-maximum
version (str) –
The version of SED sequence to use:
- ‘H’: Old Hsiao Ia SED (Hsiao, private communication)
- ‘H3’: Hsiao+2007 Ia SED
- ‘N’: Nugent+2002 Ia SED
- ‘91bg’: a SN1991bg Ia SED (Peter Nugent)
interpolate (bool) – If and day is not an integer, interpolate the spectrum linearly. Otherwise, choose nearest spectrum.
extrapolate (bool) – If True and the date is outside the range of defined SED, simply take the first/last SED to extend before/after range.

Returns:

(wave,flux):

wave (array): Wavelength in Angstroms
flux (array): arbitrarily normalized flux

Return type:

2-tuple

snpy.kcorr.kcorr(days, filter1, filter2, z, ebv_gal=0, ebv_host=0, R_gal=3.1, R_host=3.1, version='H3', photons=1)¶

Find the cross-band k-correction for a series of type Ia SED from SNooPy’s catalog. These can be thought of as “empirical” K-corrections.

Parameters:

days (float array) – epochs (t-T(Bmax)) to compute
filter1 (str) – rest-frame filter
filter2 (str) – observed filter. This can be the same as filter1, or another, redder, filter for cross-band K-corrections
z (float) – redshift
ebv_gal (float) – restframe (foreground) color excess to be applied to SED before computing K-corrections
ebv_host (float) – host-galaxy color excess to be applied to SED before computing K-correction
R_gal (float) – Ratio of selective to total absorption at V for restframe extinction.
R_host (float) – Ratio of selective to total absorption at V for host extinction.
version (str) – Which SED sequence to use. See get_SED()
photons (bool) – If True, compute fluxes in units of photons rather than energy. Default is true and should be used unless filter definition is in energy units.

Returns:

(K,mask)

K (float array): K-corrections
mask (bool array): True where K-corrections are valid.

Return type:

2-tuple

snpy.kcorr.kcorr_mangle(days, filts, mags, m_mask, restfilts, z, version='H', colorfilts=None, full_output=0, mepoch=False, **mopts)¶

Compute (cross-)band K-corrections with “mangling” using built-in library of spectral SEDs. The SEDs are first multiplied by a smooth spline such that the synthetic colors match the observed colors.

Parameters:

days (float array) – epochs (t-Tmax(B)) at which to compute K-corrections
filts (list of str) – list of observed filters
mags (2d float array) – Observed magnitude array indexed by [spectrum index,filter index]
m_mask (2d bool array) – mask array indicating valid magnitudes. Indexed by [spectrum index,filter index]
restfilts (list of str) – Rest-frame filters corresponing to filts.
z (float) – redshift
version (str) – Specify which spectral sequence to use. See get_SED().
colorfilts (list of str) – (optional) Sub set of filters to use in mangling colors (filters that have very similar effective wavelengths can make for unstable splines).
full_output (bool) – If True, output more information than just the K-corrections and mask.
mepoch (bool) – If True, a single mangling function is solved for all epochs. EXPERIMENTAL.
mopts (dict) – All additional arguments to function are sent to snpy.mangle_spectrum.mangle_spectrum2().

Returns:

if not full_output: 2-tuple (K,mask):
- K (flaot array): K-corrections for filts
- mask (bool array): mask of valid K-corrections
if full_output: 5-tuple (K,mask,anchors,factors,funcs)
- anchors (float array): wavelengths of anchor points
- factors (float array): factors corresponding to anchors
- funcs (float array): mangling function evaluated at anchors

Return type:

tuple

snpy.kcorr.kcorr_mangle2(waves, spectra, filts, mags, m_mask, restfilts, z, colorfilts=None, full_output=0, **mopts)¶

Compute (cross-)band K-corrections with “mangling” using provided spectral SEDs. The SEDs are first multiplied by a smooth spline such that the synthetic colors match the observed colors.

Parameters:

waves (list of float arrays) – Input wavelengths in Angstroms
spectra (list of float arrays) – Input fluxes in arbitrary units
filts (list of str) – list of observed filters
mags (2d float array) – Observed magnitude array indexed by [spectrum index,filter index]
m_mask (2d bool array) – mask array indicating valid magnitudes. Indexed by [spectrum index,filter index]
restfilts (list of str) – Rest-frame filters corresponing to filts.
z (float) – redshift
colorfilts (list of str) – (optional) Sub set of filters to use in mangling colors (filters that have very similar effective wavelengths can make for unstable splines).
full_output (bool) – If True, output more information than just the K-corrections and mask.
mopts (dict) – All additional arguments to function are sent to snpy.mangle_spectrum.mangle_spectrum2().

Returns:

if not full_output: 2-tuple (K,mask):
- K (flaot array): K-corrections for filts
- mask (bool array): mask of valid K-corrections
if full_output: 5-tuple (K,mask,anchors,factors,funcs)
- anchors (float array): wavelengths of anchor points
- factors (float array): factors corresponding to anchors
- funcs (float array): mangling function evaluated at anchors

Return type:

tuple

snpy.kcorr.redden(wave, flux, ebv_gal, ebv_host, z, R_gal=3.1, R_host=3.1, redlaw='ccm', strict_ccm=False)¶

Artificially redden the spectral template to simulate dust reddening, a la Cardelli et al.

Parameters:	wave (float array) – Input wavelength in Angstroms flux (float array) – arbitrarily scaled SED flux ebv_gal (float) – color excess to be applied in rest-frame (due to MW) ebv_host (floag) – color excess to be applied at host redshift z (float) – redshift of the host extinction R_gal (float) – Ratio of total to selective absoption in V for restframe component of extinction. R_host (float) – Ratio of total to selective absorption in V for host frame extinction. redlaw (str) – Form of the dust extinction curve. Possible values are ‘ccm’, ‘f99’, or ‘fm07’. See `snpy.utils.deredden`.
Returns:	reddened flux.
Return type:	float array

snpy.mangle_spectrum module¶

Color-matching: modifying a spectrum by multiplication of a smooth function in order to reproduce the observed photometry. A mangler class is used to do all the heavy lifting of fitting a smooth function. A base class called function is provided and should be sub-classed to implement new smoothing functions. So far, there’s tension splines and CCM.

class snpy.mangle_spectrum.f_ccm(parent, tension=None, gradient=False, slopes=None, verbose=False)¶

Bases: snpy.mangle_spectrum.function

The Cardelli, Clayton, and Mathis (1989) reddening law as a smooth fucntion. This would be what dust does to a spectrum, so is a good guess, but has much less freedom than tension splines.

class snpy.mangle_spectrum.f_spline(parent, s=0, gradient=False, slopes=None, verbose=False, log=False)¶

Bases: snpy.mangle_spectrum.function

Spline mangler. Splines are controlled by a smoothing parameter. The higher the smoothing, the less curvature the spline can have. This is good for keeping the spline from “wigglig” too much.

class snpy.mangle_spectrum.f_tspline(parent, tension=None, gradient=False, slopes=None, verbose=False, log=False)¶

Bases: snpy.mangle_spectrum.function

Tension spline mangler. Tension splines are controlled by a tension parameter. The higher the tension, the less curvature the spline can have. This is good for keeping the spline from “wigglig” too much.

class snpy.mangle_spectrum.function(parent)¶

A function object that represents a way of making a smooth multiplication on the spectrum, thereby “mangling” it. The function has an evaluate function as well as a wrapper that is suitable for using with mpfit.

init_pars()¶: Reset the parameters of the function to initial values. This should cause the function to return the identity ( f(x) = 1.0).

setup()¶: Do any initial setup.

snpy.mangle_spectrum.mangle_spectrum2(wave, flux, bands, mags, fixed_filters=None, normfilter=None, z=0, verbose=0, anchorwidth=100, method='tspline', xtol=1e-06, ftol=1e-06, gtol=1e-06, init=None, **margs)¶

Given an input spectrum, multiply by a smooth function (aka mangle) such that the synthetic colors match observed colors.

Parameters:

wave (float array) – Input wavelengths in Angstroms
flux (float array) – Input fluxes in arbitrary units
bands (list of str) – list of observed filters
mags (float array) – Observed magnitudes
m_mask (bool array) – mask array indicating valid magnitudes.
fixed_filters (str or None) – If not None, append fake filters on the red and/or blue end of the spectrum, keeping their mangled flux fixed. Specify ‘red’, ‘blue’, or ‘both’.
normfilter (str) – If specified, the resulting mangled spectrum is normalized such that the flux through normfilter is the same as the input spectrum.
z (float) – redshift
verbose (bool) – output extra info.
anchorwidth (float) – width of the “fixed filters” at either end of the SED in Angstroms.
method (str) – specify the method (function form) with which to mangle the spectrum. ‘tspline’ for tension spline or ‘ccm’ for the CCM reddening law.
xtol,ftol,gtol (float) – used to define the tolorance for the goodness of fit. See scipy.optimize.leastsq for meaning of these parameters.
init (list/array) – initial values for the mangle parameters.
margs (dict) – All additional arguments to function are sent to the mangle_spectrum.Mangler class.

class snpy.mangle_spectrum.mangler(wave, flux, method, normfilter=None, z=0, **margs)¶

Given a spectrum and spectrum object, find the best set of a function’s paramters, such that the function multiplied by the spectrum produces the colors specified.

create_anchor_filters(bands, anchorwidth)¶

Given a set of filters in bands, create two fake filters at either end to serve as anchor filters.

Parameters:	bands (list of str) – The list of filters to construct colors from anchorwidth (float) – distance from reddest and bluest filter in Angstroms.
Returns:	None

Effects:: fset is updated to include two new filters: ‘red_anchor’ and ‘blue_anchor’

get_colors(bands)¶

Given a set of filters, determine the colors of the mangled spectrum for the current set of function parameters. You’ll get N-1 colors for N bands and each color will be bands[i+1]-bands[i]

Parameters:	bands (list of str) – The list of filters to construct colors from
Returns:	colors
Return type:	2d array

get_mflux()¶: Given the current paramters, return the mangled flux.

solve(bands, colors, fixed_filters=None, anchorwidth=100, xtol=1e-10, ftol=0.0001, gtol=1e-10, init=None)¶

Solve for the mangling function that will produce the observed colors in the filters defined by bands.

Parameters:

bands (list of str) – The list of filters to construct colors from
colors (float array) – the colors to match. If 1d, the N-1 colors should correspond to bands[i-1]-bands[i], if 2d, the first index should reflect spectrum number.
fixed_filters (2-tuple or None) – The filters whose control points should remain fixed. If None, two fake filters will be created.
anchorwidth (float) – If making fake filters, they will be spaced this many Angstroms from the bluest and reddest filters (default 100).
ftol, gtol (xtol,) – see scipy.optimize.leastsq.

Table Of Contents

Previous topic

Next topic

This Page

snpy package API¶

Module contents¶

Subpackages¶

Submodules¶

snpy.sn module¶

snpy.lc module¶

snpy.model module¶

snpy.kcorr module¶

snpy.mangle_spectrum module¶