snpy.utils package¶
Submodules¶
snpy.utils.GLOEs module¶
GLOESpy
Algorithm: Barry Madore Python version: Chris Burns
- Requires: Numeric,
- fit_poly (http://www.ociw.edu/Code/python/burns-python-scripts/fit_poly.py)
A routine for generating a smooth 1D or 2D interpolation based on irregularly sampled data. The basic idea is simple:
- You’ve got a bunch of data (x, y +/- dy)
- consider a point where you want to interpolat (x0)
- generate a normalized Gaussian window function W(x0,sigma) centered at x0 with a certain width sigma.
- weight the data like W(x0,sigma)/dy
- Fit a polynomial at x0 and use that to interpolated the value y0.
- Repeat for each point x0.
For a 2D surface, you use an elliptical Gaussian window function and fit a 2D polynomial.
-
class
snpy.utils.GLOEs.line(x, y, dy, sigma=None, N=None)¶ A class to represent a line of data. The construtor takes x,y,dy data as arguments (and optionally the smoothing length). Member functions allow the user to interpolate on the line.
-
chisq(sigma=None, N=None)¶ Compute chisq for a supplied sigma or one stored in the instance.
-
eval(x, sigma=None, N=None)¶
-
find_N(low, high)¶ Given a range of N (low, high), compute rchisq for each and return the smoothing length that gives rchisq closest to 1.
-
find_sigma(low, high, ds)¶ Given a range of sigmas (low,high) and interval (ds), compute rchisq for each and return the smoothing length that gives rchisq = 1 (or as close as possible).
-
-
snpy.utils.GLOEs.smooth(x, y, weight, xeval, sigma=None, N=None)¶ Given a set of x and y points, with associated internal errors in y given by erry, find a smothing esimate of the data using Barry’s GLOEs algorithm evaluated at the points in xeval. The Gaussian window function will have a sigma=sigma.
-
snpy.utils.GLOEs.smooth2d(x, y, z, wt, xeval, yeval, sigmax=None, sigmay=None, Nx=10, Ny=10, tol=0)¶ Given a set of x, y, z points, with associated internal errors in z given by 1/wt, find a smothing esimate of the data using Barry’s GLOEs algorithm evaluated at the points in xeval, yeval. The Gaussian window function will have a sigma=sigmax in the x-direction and sigmay in the y-direction.
-
class
snpy.utils.GLOEs.surface(x, y, z, dz, sigmax=None, sigmay=None, Nx=None, Ny=None)¶ A class to represent a surface of data. The construtor takes x,y,z,dz data as arguments (and optionally the smoothing lengths). Member functions allow the user to interpolate on the surface.
-
eval(x, y, sigmax=None, sigmay=None, Nx=None, Ny=None, tol=0)¶
-
snpy.utils.IRSA_dust_getval module¶
A module to make WEB querries to the IRSA Schlegel dust map calulator and extract E(B-V)
-
snpy.utils.IRSA_dust_getval.get_dust_RADEC(ra, dec, calibration='SF11')¶ Query IRSA with given ra and dec to get the E(B-V). To remain compatible with dust_getval module, return a list (dust_getval results an array). You can specify calibration of “SF11” or “SFD98”
-
snpy.utils.IRSA_dust_getval.get_dust_sigma_RADEC(ra, dec, calibration='SF11')¶ Query IRSA with given ra and dec to get the error in E(B-V). You can specify calibration of “SF11” or “SFD98”
snpy.utils.deredden module¶
This modules implements several reddening laws: extinction as a function of wavelength. They are the following:
- ccm: Cardelli, Clayton & Mathis (1989)
- fm: Fitzpatrick (1999).
- fm07_full: The fully-parametrized Fitzpatrick and Masa (2007) function.
- fm07: Average Fitzpatric & Masa (2007) for MW.
- nataf: Experiemental version of CCM from David Nataf.
-
snpy.utils.deredden.R_z(wave, z, R_V=3.1, strict_ccm=0)¶ Compute host reddening law for effective observed wavelength wave, at redshift z, assuming R_V.
-
snpy.utils.deredden.ccm(wave, strict_ccm=0)¶ Returns the Cardelli, Clayton, and Mathis (CCM) reddening curve.
Parameters: - wave (float array) – wavelength in Angstroms
- strict_ccm (bool) – If True, return original CCM (1989), othewise apply updates from O’Donnel (1994)
Returns: 2-tupe – The coeffients such that
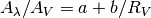
Return type: a,b
-
snpy.utils.deredden.fm(wave, R_V=3.1, avglmc=False, lmc2=False)¶ Deredden a flux vector using the Fitzpatrick (1999) parameterization. The R-dependent Galactic extinction curve is that of Fitzpatrick & Massa (Fitzpatrick, 1999, PASP, 111, 63; astro-ph/9809387 ). Parameterization is valid from the IR to the far-UV (3.5 microns to 0.1 microns). UV extinction curve is extrapolated down to 912 Angstroms.
Parameters: - wave (float array) – wavelength in Angstroms
- R_V (float) – The ratio of total to selective extionction
- avglmc (bool) – If True, the default fit parameters c1,c2,c3,c4,gamma,x0 are set to the average values determined for reddening in the general Large Magellanic Cloud (LMC) field by Misselt et al. (1999, ApJ, 515, 128)
- lmc2 (bool) – if True, the fit parameters are set to the values determined for the LMC2 field (including 30 Dor) by Misselt et al.
Returns: 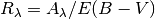
Return type: foat array
-
snpy.utils.deredden.fm07(wave, R_V=3.1)¶ Average reddening law from Fitzpatrick & Massa (2007). This includes a variation with R(V) and uses the correlation between R(V) and k_NIR to make a one-parameter curve (keeping all other curve parameters fixed. Caveats abound. Read the paper!
Parameters: - wave (float array) – wavelength in Angstroms
- R_V (float) – ratio of total-to-selective absorption.
Returns: R_V – A_V/E(B-V)
Return type: float array
-
snpy.utils.deredden.fm07_full(wave, x0, gamma, c1, c2, c3, c4, c5, o1, o2, o3, R, iscale, ipower=1.84)¶ The fully-parametrized Fitzpatrick & Massa reddening curve.
Parameters: - wave (float array) – wavelength in Angstroms
- x0 (float) – centroid of 2200 A bump (microns)
- gamma (float) – width of 2200 bump (microns)
- c1 (float) – Intercept of linear UV extinction
- c2 (float) – Slope of linear UV extinction
- c3 (float) – Strength of 2200 A bump
- c4 (float) – UV curvature
- c5 (float) – Onset of UV curvatrue (microns)
- o1,o2,o3 (float) – optical spline points
- R (float) – A_V/E(B_V)
- iscale – NIR scale
- ipower – power-law index for NIR.
Returns: E(V-lambda)/E(B-V)
Return type: foat array
-
snpy.utils.deredden.nataf(wave, R_V=3.1, strict_ccm=False)¶ CCM modified by David Nataf, private communication.
Parameters: - wave (float array) – wavelength in Angstroms
- strict_ccm (bool) – If True, return original CCM (1989), othewise apply updates from O’Donnel (1994)
Returns: 2-tupe – The coeffients such that
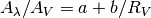
Return type: a,b
-
snpy.utils.deredden.poly(x, c)¶
-
snpy.utils.deredden.unred(wave, flux, ebv, R_V=3.1, z=0, redlaw='ccm', strict_ccm=0)¶ de-redden (or redden, if you set ebv < 0) a spectrum using color excess E(B-V). Optionally, you can redshift the spectrum. You can choose between the Cardelli, Clayton and Mathis, (redlaw=’ccm’), Fitzpatrick (1999) law (redlaw=’fm’), . If using ccm, you can either use the default CCM modified by O’Donnel (1994) or use the script CCM by specifying strict_ccm=True.
Parameters: - wave (float array) – wavelenths in Angstroms
- flux (float array) – flux in arbitrary units
- ebv (float) – color excess E(B-V)
- R_V (float) – ratio of total-to-selective absorption
- z (float) – redshift the spectrum by this amount before applying reddening law.
- redlaw (str) – Choice of particular reddening law. Currently we have: ‘ccm’: Cardelli, Clayton & Mathis (1989) + O’Donnel (1994) ‘fm’ or ‘f99’: Fitzpatrick (1999) ‘fm07’: Fitzpatrick & Masa (2007)
- srict_ccm (bool) – If True and redlaw=’ccm’, ignore changes by O’Donnel (1994)
Returns: (uflux, a, b) uflux: un-reddened flux a,b: The equivalent of the CCM a and b parameters.
Return type: 3-tuple
-
snpy.utils.deredden.unred_fm(wave, flux, ebv, R_V=3.1, z=0, avglmc=False, lmc2=False)¶ Deredden by the Fitzpatrick (1999) Law
-
snpy.utils.deredden.unred_fm07(wave, flux, ebv, R_V=3.1, z=0)¶ Deredden by the Fitzpatrick & Massa (2007) Law
snpy.utils.fit1dcurve module¶
This module provices an abstract class whose purpose is fitting a 1D curve using several different methods (polynomial, splines, Gaussian processes), but providing a consistent API for evalutation and computing derivatives, extrama, etc.
-
class
snpy.utils.fit1dcurve.GaussianProcess(x, y, dy, mask=None, **args)¶ Bases:
snpy.utils.fit1dcurve.oneDcurve-
__call__(x)¶ Interpolate at point [x]. Returns a 3-tuple: (y, mask) where [y] is the interpolated point, and [mask] is a boolean array with the same shape as [x] and is True where interpolated and False where extrapolated
-
deriv(x, n=1)¶ Returns the nth derivative of the function at x.
-
domain()¶
-
draw()¶ Generate a random realization of the spline, based on the data.
-
error(x)¶ Returns the error in the interpolator at points [x].
-
find_extrema(xmin=None, xmax=None)¶ Find the position and values of the maxima/minima. Returns a tuple: (roots,vals,ypps) where roots are the x-values where the extrema occur, vals are the y-values at these points, and ypps are the 2nd derivatives. Optionally, only search for roots between xmin and xmax
-
func(x)¶
-
help()¶
-
intercept(y)¶ Find the value of x for which the interpolator goes through [y]
-
rchisquare()¶
-
reset_mean()¶
-
-
class
snpy.utils.fit1dcurve.HyperSpline(x, y, dy, mask=None, **args)¶ Bases:
snpy.utils.fit1dcurve.oneDcurve-
__call__(x)¶ Interpolate at point [x]. Returns a 3-tuple: (y, mask) where [y] is the interpolated point, and [mask] is a boolean array with the same shape as [x] and is True where interpolated and False where extrapolated
-
deriv(x, n=1)¶ Returns the nth derivative of the function at x.
-
domain()¶
-
draw()¶ Generate a random realization of the spline, based on the data.
-
find_extrema(xmin=None, xmax=None)¶ Find the position and values of the maxima/minima. Returns a tuple: (roots,vals,ypps) where roots are the x-values where the extrema occur, vals are the y-values at these points, and ypps are the 2nd derivatives. Optionally specify the range over which maxima are valid.
-
help()¶
-
intercept(y)¶ Find the value of x for which the interpolator goes through [y]
-
rchisquare()¶
-
reset_mean()¶
-
-
snpy.utils.fit1dcurve.Interpolator(type, x, y, dy, mask=None, **args)¶ Convenience function that returns a 1D interpolator of the given [type] if possible.
-
class
snpy.utils.fit1dcurve.Polynomial(x, y, dy, mask=None, **args)¶ Bases:
snpy.utils.fit1dcurve.oneDcurve-
__call__(x)¶ Interpolate at point [x]. Returns a 3-tuple: (y, mask) where [y] is the interpolated point, and [mask] is a boolean array with the same shape as [x] and is True where interpolated and False where extrapolated
-
deriv(x, n=1)¶ Returns the nth derivative of the function at x.
-
domain()¶ Returns the valid domain of the polynomial.
-
draw()¶ Generate a random realization of the spline, based on the data.
-
find_extrema(xmin=None, xmax=None)¶ Find the position and values of the maxima/minima. Returns a tuple: (roots,vals,ypps) where roots are the x-values where the extrema occur, vals are the y-values at these points, and ypps are the 2nd derivatives. optionally, restrict roots to between xmin, and xmax
-
help()¶
-
intercept(y)¶ Find the value of x for which the interpolator goes through [y]
-
rchisquare()¶
-
reset_mean()¶
-
-
class
snpy.utils.fit1dcurve.Spline(x, y, dy, mask=None, **args)¶ Bases:
snpy.utils.fit1dcurve.oneDcurve-
__call__(x)¶ Interpolate at point [x]. Returns a 3-tuple: (y, mask) where [y] is the interpolated point, and [mask] is a boolean array with the same shape as [x] and is True where interpolated and False where extrapolated
-
add_knot(x)¶ Add a knot point at x. The task parameter is automatically set to -1 as a result.
-
delete_knot(x)¶ Delete knot closest to x. The task parameter is automatically set to -1 as a result.
-
deriv(x, n=1)¶ Returns the nth derivative of the function at x.
-
domain()¶
-
draw()¶ Generate a random realization of the spline, based on the data.
-
find_extrema(xmin=None, xmax=None)¶ Find the position and values of the maxima/minima. Returns a tuple: (roots,vals,ypps) where roots are the x-values where the extrema occur, vals are the y-values at these points, and ypps are the 2nd derivatives. Optionall, search only betwwen xmin and xmax.
-
help()¶
-
intercept(y)¶ Find the value of x for which the interpolator goes through [y]
-
move_knot(x, xnew)¶ Move knot closest to x to new location xnew. The task parameter is automatically set to -1 as a result.
-
rchisquare()¶
-
reset_mean()¶
-
-
snpy.utils.fit1dcurve.list_types()¶ Returns a list of 1D interpolators that are defined at load-time.
-
class
snpy.utils.fit1dcurve.oneDcurve(x, y, ey, mask=None, **args)¶ Base class for 1D interpolators. Each subclass inherits the basic structure defined below, but is responstible for implementing the different methods.
-
DW()¶ Returns the Durvin-Watson statistic for current parameters.
-
__call__(x)¶ Return the interpolation at point(s) x.
Parameters: x (float array or scalar) – Location at which to compute interpolant Returns: (y, mask) - y (float array or scalar): interpolant. type matches input x
- mask (float array or scalar): False indicates extrapolation
Return type: 2-tuple
-
chisquare()¶ Returns the chi-square statistic for current parameters.
-
deriv(x, n=1)¶ Returns the nth derivative of the function at x.
Parameters: - x (float array or scalar) – location at which to compute derivative
- n (int) – order of the derivative to compute
Returns: derivative at x (type matches input x)
Return type: float array or scalar
-
domain()¶ Return the valid domain for this model
Returns: (xmin, xmax): the domain of the function. Return type: 2-tuple
-
draw()¶ Generate a Monte Carlo realization of the data. Interpolator will now give values based on this realization.
-
error(x, N=50)¶ Estimate the error in the interpolant at the point x.
Parameters: - x (float array or scalar) – location at which to compute error
- N (int) – If bootstrap is required, number of iterations.
Returns: the error (type matches input x)
Return type: float array or scalar
-
find_extrema(xmin=None, xmax=None)¶ Find the position and values of the maxima/minima.
Parameters: - xmin (float) – only consider extrema on interval (xmin,xmax)
- xmax (float) – only consider extrema on interval (xmin,xmax)
Returns: (roots,vals,curvs)
- roots (float array or None): locations where derivative is zero or None if no extrma on interval
- vals (float array or None): interpolant at roots
- curvs (float array or None): sign of curvature at roots. -1 if concave down (maximum), +1 if concave up (minimum)
Return type: 3-tuple
-
help()¶ Provide a help string.
-
interact()¶ If we have the InteractiveFit module, spawn an interactive fitter.
Returns: InteractiveFit.InteractiveFit instance or None
-
intercept(y)¶ Find the value of x for which the interpolator goes through y
Parameters: y (float) – value of y for which we wish to know x Returns: value(s) of x at y or None if function does not cross y on domain Return type: float array or None
-
maskid(i)¶ Mask the point based on index.
Parameters: i (int) – index of point to mask. Returns: None - Effects:
- self.mask is updated
-
maskpoint(x, y)¶ Mask the point closest to (x,y).
Parameters: - x (float) – (x,y) point to mask out
- y (float) – (x,y) point to mask out
Returns: None
- Effects:
- self.mask is updated
-
maskresids(absclip=None, sigclip=None)¶ Mask data outside a range of residuals.
Parameters: - absclip (float) – mask out data with residuals > absclip
- sigclip (float) – mask out data with residuals > sigclip*sigma
Returns: None
- Effects:
- self.mask is updated
-
num_real_keep= 100¶
-
rchisquare()¶ Returns the reduced chi-square statistic for current parameters.
-
reset_mean()¶ Reset to the original data after using draw()
-
residuals(mask=True)¶ Compute the residuals (data - model) for current parameters.
Parameters: mask (bool) – If True, omit masked values from residuals Returns: residuals Return type: float array
-
rms()¶ Returns RMS of residuals for current parameters.
-
-
snpy.utils.fit1dcurve.regularize(x, y, ey)¶ Given x,y,dy data, make sure the data is strictly monatonic with respect to x and elimitate repeated values.
Parameters: - x (float array) – input independent variable
- y (float array) – input dependent variable
- ey (float array) – input error in dependent variable
Returns: (x,y,ey) output values of x,y,ey, where duplicate x are averaged and x is strictly monotonically increasing.
Return type: 3-tuple
snpy.utils.InteractiveFit module¶
This class lets you interactively fit using the fit1dcurve classes.
-
class
snpy.utils.InteractiveFit.InteractiveFit(interp, title=None, figsize=None, fignum=None, draw=True, xlabel='X', ylabel='Y', extra_bindings={})¶ -
draw()¶ Just an alias to self.mp.draw.
-
help()¶
-
plot_params()¶
-
plot_stats()¶ plots the statistics of the fit.
-
redraw()¶ Redraw the graph
-
redraw_x()¶ Redraw the little red X’s if needed
-
set_bindings()¶ Sets the bindings to the figure canvas.
-
setup_graph(draw=True)¶
-
snpy.utils.fit_lc module¶
This module fits a parameterized function for a SNIa light-curve with one or two peaks. Taken from M. Stritzinger’s PhD thesis, which was adapted from Contardo, G., Leibundgut, B., & Vacca, W. D. 2000, A&A, 359, 876.
-
snpy.utils.fit_lc.Ialcn(t, par, n)¶
-
snpy.utils.fit_lc.d_Ialcn_dp(par, t, y, dy, n)¶
-
snpy.utils.fit_lc.d_Ialcn_dt(t, par, n)¶
-
snpy.utils.fit_lc.fit_lc(t, mag, e_mag, ngauss=1, maxiter=10000, p0=None, Tmax=None)¶ Fit a light-curve to the parameterized model. t = time, mag = magnitudes, e_mag = error in magnitudes. If ngauss=1, fit a single-peaked LC, if ngauss=2, fit a 2-peaked one.
-
snpy.utils.fit_lc.guess_parsn(t, n, mag, Tmax=None)¶
-
snpy.utils.fit_lc.wrap_Ialcn(p, x, y, dy, n)¶
snpy.utils.fit_lc2 module¶
This module fits a parameterized function for a SNIa light-curve with one or two peaks. Taken from M. Stritzinger’s PhD thesis, which was adapted from Contardo, G., Leibundgut, B., & Vacca, W. D. 2000, A&A, 359, 876.
-
snpy.utils.fit_lc2.Ialc1(t, m0, gamma, t0, g0, sig0, theta)¶ The parametric function with one maximum we want to fit.
-
snpy.utils.fit_lc2.Ialc2(t, m0, gamma, t0, g0, sig0, t1, g1, sig1, theta)¶ The parametric function with two maxima we want to fit.
-
snpy.utils.fit_lc2.d_Ialc1_dp(t, p)¶
-
snpy.utils.fit_lc2.d_Ialc1_dt(t, m0, gamma, t0, g0, sig0, tau, theta)¶ First derivative of Ialc1 wrt t.
-
snpy.utils.fit_lc2.d_Ialc2_dp(p, t, mag, e_mag)¶
-
snpy.utils.fit_lc2.d_Ialc2_dt(t, m0, gamma, t0, g0, sig0, t1, g1, sig1, tau, theta)¶ First derivative of Ialc2 wrt t.
-
snpy.utils.fit_lc2.fit_lc(t, mag, e_mag, ngauss=1, maxiter=10000, p0=None, Tmax=None)¶ Fit a light-curve to the parameterized model. t = time, mag = magnitudes, e_mag = error in magnitudes. If ngauss=1, fit a single-peaked LC, if ngauss=2, fit a 2-peaked one.
-
snpy.utils.fit_lc2.guess_pars1(t, mag, Tmax=None)¶ Based on the input light-curve, guess the likely paramters.
-
snpy.utils.fit_lc2.guess_pars2(t, mag, Tmax=None)¶ Based on the input light-curve, guess the likely paramters.
-
snpy.utils.fit_lc2.wrap_Ialc1(p, x, y, dy)¶
-
snpy.utils.fit_lc2.wrap_Ialc2(p, x, y, dy)¶
snpy.utils.fit_poly module¶
Fit 1D and 2D polynomials of order k to a set of data points. Actually, they’re McLaren series in 1 and 2 variables.
Written by Chris Burns Obfuscated by Dan Kelson.
-
snpy.utils.fit_poly.divz(x, y=1, repl=0.0, out=<type 'numpy.float32'>, tol=0)¶
-
snpy.utils.fit_poly.fac(N)¶
-
snpy.utils.fit_poly.fit2Dpoly(x, y, z, w, k=1, x0=0, y0=0)¶ Fit a 2D McLaren series of degree k to some data (x,y,z) with weights w, centered on the point (x=x0, y=y0). Returns the tuple (coeff, err). Coeff are the coefficients of the series in the following order. Let f[i,j](x0,y0) be the ith partial derivative of f w.r.t. x and jth partial derivative of f w.r.t y evaluated at (x0,y0). The Coeff is
f[0,0](x0,y0), f[1,0](x0,y0), ..., f[k,0](x0,y0), f[0,1](x0,y0), f[1,1](x0,y0), ..., f[k,1](x0,y0), ... f[0,k](x0,y0), f[1,k](x0,y0), ..., f[k,k](x0,y0)
-
snpy.utils.fit_poly.fitpoly(x, y, w, k=1, x0=0)¶ Fit a 1D McLaren series of degree k to some data (x,y) with weights w, centered on the point x=x0. Returns (coeff,err) which are the coefficients of the series: f(x0), f’(x0), f’‘(x0), ... and the associated errors.
-
snpy.utils.fit_poly.fitsvd(A, b)¶
-
snpy.utils.fit_poly.legendre(x, y, u)¶ Given the length of x and y, determine the legendre interpolating polynomial and evaluate at u
-
snpy.utils.fit_poly.poly(x, x0, soll)¶ Compute the polynomial from the solution.
-
snpy.utils.fit_poly.poly2D(x, y, x0, y0, soll)¶
snpy.utils.fit_spline module¶
This module provides some helper functions for fitting a spline to Supernova data.
-
snpy.utils.fit_spline.K2(x, tck)¶ compute the square curvature of a spline2 at point x
-
snpy.utils.fit_spline.find_extr(tck, numpoints=1000)¶
-
snpy.utils.fit_spline.fit_spline(t, m, e_m, knots=None, k=1, s=None, fitflux=0, zpt=0, tmin=-10, tmax=100, task=-1)¶ Fit a spline to a set of lightcurve data (t,m,e_m). The rest of the arguments are the same as make_spline() above. The spline is then evaluated at one day intervals from t[0] to t[-1] and returned as a two-tuple (time,mag).
-
snpy.utils.fit_spline.interp_spline(t, m, e_m, eval_t, knots=None, k=1, s=None, fitflux=0, zpt=0, tmin=-10, tmax=100, task=-1, tol=0.1)¶ Same as fit_spline, except that you decide on the interpolated times. Good for making color estimates when data in different bands in at different epochs. In this case, only the interpolated magnitudes are returned.
-
snpy.utils.fit_spline.make_spline(t, m, e_m, knots=None, k=1, s=None, fitflux=0, zpt=0, tmin=None, tmax=None, task=-1, anchor_dist=[5.0, 5.0], slopes=[None, None])¶ A wrapper around splrep that makes sure the independent variable is monotonic and non-repeating. Required arguments: time (t), magnitudes (m) and errors (e_m). If knots are specified, use them (if task==-1), otherwise, they are computed from -10 days to 100 days in 10-day increments. k is the spline order (default 1) and s is the smoothing factor, as per splrep. If fitflux is nonzero, convert magnitudes to flux (using provided zpt). tmin and tmax should be set to the limits of the spline.
-
snpy.utils.fit_spline.make_spline2(t, m, e_m, k=3, fitflux=0, zpt=0, tmin=-10, tmax=100, adaptive=0, max_curv_fac=10, **args)¶ A wrapper around spline2 that makes sure the independent variable is monotonic and non-repeating. Required arguments: time (t), magnitudes (m) and errors (e_m). k is the spline order (default 3) If fitflux is nonzero, convert magnitudes to flux (using provided zpt). tmin and tmax should be set to the limits of the spline.
snpy.utils.radec2gal module¶
Module for computing the galactic coordinates from stored RA/DEC coordinates. If we have astropy,use that, otherwise try NED calculator
-
snpy.utils.radec2gal.radec2gal(ra, dec)¶
snpy.utils.redlaw module¶
A module to compute the reddening law based on specified filters.
The basic problem is that we observe in a particular filter and are correcting by the color in two other filters. So, we want to make the following correction:
m1_true = m1_obs - R*E(m2 - m3)
where E(m2 - m3) = m2_obs - m3_obs - (m2_true - m3_true)
is the color excess through filters 2 and 3. We want to be able to compute R and also take this value of R and convert back to the CCM R_V parameter.
-
snpy.utils.redlaw.R_lambda(f, Rv, EBV, redlaw='ccm')¶ A fast implementation based on bivariate splines.
-
snpy.utils.redlaw.R_to_Rv(f1, f2, f3, R, EBV=0.01, day=0, strict_ccm=0, version='H3')¶ Same as Rv_toR, but work in reverse to find Rv, given R
-
snpy.utils.redlaw.Rv_to_R(f1, f2, f3, Rv, EBV=0.01, day=0, redlaw='ccm', strict_ccm=0, version='H3')¶ Convert from R_V and optionally EBV to an observed R through filter f1, corrected by f2-f3 color. You can choose which day the SN SED should be (default day 0, max). You can also specify which reddening law to use: redlaw=’ccm’ for Cardelli et al., or redlaw=’fm’ for Fitzpatric and Malla (1999), If redlaw=’ccm’, you can specify whether we should use the strict CCM relation (default no). Finally, you an choose which SED sequence to use: ‘H’, ‘H3’, or ‘91bg’ (default H3).
snpy.utils.zCMB module¶
Module for computing the CMB redshift from the heliocentric redshift and coordinates. For now, uses NED calculatro, but maybe later will do all the math, so we don’t need the interweb
-
snpy.utils.zCMB.z_cmb(z_hel, ra, dec)¶
Module contents¶
A collection of utility mocules.