MCMC Fitting¶
While the LM fitter can give adequate fits to most light-curves, there are times when it would be useful to impose priors on the various parameters of the fit. Such cases might be:
- The
color_modelis used on an object whose reddening is very low, thereby making the model insensitive toRv_host. - The supernova has a very poorly sampled light-curve (maybe only one point) and you want to use a prior on the stretch and/or time of maximum.
- You wish to combine the SN distance estimate with another, independent, estimate.
- etc.
Doing the Fit¶
Begin fitting in the usual way using the fit() function (see
Doing the Fit). This will provide a good starting point for the MCMC
chains. Next, use fitMCMC() to start the MCMC simulation. The
calling sequence is much the same as fit(), with some extra
arguments to control the MCMC sampling and the ability to assign priors to the
model parameters.
Priors¶
When calling fitMCMC(), you can assign priors to any of the
model parameters by assigning them as arguments (similar to how one kept a
parameter fixed using fit(). There are three ways to do so:
- Three built-in priors (Normal, Exponential, and Uniform) can be
specified by strings. The string should begin with
N,E, orUto specify Normal, Exponential, or Uniform respectively. Arguments for the prior then follow as a comma-separated list:N,mu,sigma: Normal distribution with meanmuand standard deviationsigma. Example:"N,0,0.5".E,tau: Positive exponential with scaletau. Example:"E,0.7".U,lower,upper: Uniform distribution betweenlowerandupper. Example:"U,0,10".
- A floating-point scalar can be specified to keep the parameter fixed at the given value.
- A python function that takes a single argument (the value of the parameter) and returns the log-probability.
Some models also have built-in priors at work. At the moment, the
color_model color_model has these kinds of priors, which are
used on the reddening law Rv_host. There are currently three priors that
can be used: uniform, mix, and bin. These correspond to a uniform,
Gaussian mixture model, and Normal distribution binned by color. They are
chosen by specifying the rvprior argument to fitMCMC().
Examples¶
First, we load in some data, choose the color_model
and fit with not constraints:
In [1]: s = get_sn('SN2006ax.txt')
In [3]: s.choose_model('color_model', stype='st')
In [4]: s.fit()
[Full Traceback excluded]
RuntimeError: Error: Covariance Matrix is singular. Either two or more
parameters are degenerate or the modelhas become insensitive to one or more
parameters.
The fit failed because 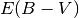 is small for this object, so the model
is insensitive to
is small for this object, so the model
is insensitive to 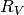 . We can proceed by fixing
. We can proceed by fixing 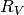 :
:
In [5]: s.fit(Rv=2.0)
In [6]: s.summary()
--------------------------------------------------------------------------------
SN SN2006ax
z = 0.017 ra=171.01442 dec=-12.29144
Data in the following bands: B, g, i, H, K, J, r, u, V, Y,
Fit results (if any):
Observed B fit to restbad B
Observed g fit to restbad g
Observed i fit to restbad i
Observed H fit to restbad H
Observed K fit to restbad K
Observed J fit to restbad J
Observed r fit to restbad r
Observed u fit to restbad u
Observed V fit to restbad V
Observed Y fit to restbad Y
EBVhost = 0.033 +/- 0.002
Rv = 2.000 +/- 0.000
Bmax = 14.922 +/- 0.006
Tmax = 53827.078 +/- 0.029
st = 0.987 +/- 0.004
Keeping 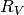 fixed has allowed us to fit the rest of the parameters
(note the small value for
fixed has allowed us to fit the rest of the parameters
(note the small value for EBVhost. But if we want to be realistic and allow
for some uncertainty in the value of 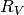 , we can use the
, we can use the
fitMCMC() method:
In [6]: s.fitMCMC(bands=['u','B','V','g','r','i','Y','J','H'], R_V="N,2.3,0.9")
In [7]: s.summary()
--------------------------------------------------------------------------------
SN SN2006ax
z = 0.017 ra=171.01442 dec=-12.29144
Data in the following bands: B, g, i, H, K, J, r, u, V, Y,
Fit results (if any):
Observed B fit to restbad B
Observed g fit to restbad g
Observed i fit to restbad i
Observed H fit to restbad H
Observed K fit to restbad K
Observed J fit to restbad J
Observed r fit to restbad r
Observed u fit to restbad u
Observed V fit to restbad V
Observed Y fit to restbad Y
EBVhost = 0.017 +/- 0.009
Rv = 2.207 +/- 1.051
Bmax = 14.963 +/- 0.033
Tmax = 53827.078 +/- 0.018
st = 0.986 +/- 0.003
As you can see, allowing 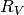 has increased the uncertainty in
has increased the uncertainty in
Bmax, as one would epect.