Fitting with Levenberg-Marquardt¶
This is the faster way to fit light-curves in SNooPy. It uses the non-linear
least-squares [Levenberg-Marquardt] algorithm (LMA). It minimizes the
variance-weighted residuals of the data from the model. Specifically,
SNooPy uses the scipy.optimze.leastsq function under the hood.
Doing the Fit¶
The fit() function is a member of the sn class.
The first argument is a list of observed filters to fit (or by default,
fit them all). Following this argument, you can specify values for
any of the parameters, which will keep them fixed during the iteration:
Tmax, dm15, st, EBVhost, DM, and any of the fmax.
By default, the fitter will try to fit the observed filter set with
the same rest-band filters. It is therefore important that your filter
names match the filters provided by the templates: Bs,Vs,Rs,Is
(for [Prieto+2006] templates) or u,B,V,g,r,i,Y,J,H
(for CSP templates). If your observed filter does not match any of
these (either because you are working at high-z and want to do a cross-band
K-correction, or are working in a different photometric system), you
need to specify the restbands for each observed filter (restbands
is a member variable that acts like a python dictionary and maps observed
filters to rest filters). Here is a short example:
In [1] s = get_sn('04D1oh')
In [2] s.restbands['g_m'] = 'B' ;# Fit observed g_m data with 'B' (CSP)template
In [3] s.fit(['g_m'], EBVhost=0, dm15=1.1)
In [4] s.fit(['g_m'], EBVhost=0)
In [5] s.restbands['r_m'] = 'V'; s.restbands['i_m'] = 'r'; s.restbands['Jc'] = 'i'
In [6] s.fit(['g_m','r_m','i_m','Jc'], dm15=s.dm15, Tmax=s.Tmax)
In [7] s.fit(['g_m','r_m','i_m','Jc'])
In [8] s.save(s, "my_lovely_fit.snpy")
On line 1, we make a new instance. On line 3, we decide to fit the
megacam g filter with a rest-frame CSP B template. On line 3, we fit
only the g_m filter and therefore restrict EBVhost to 0
(since we don’t have any color information). We can also fix
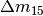 for a first attempt at a fit (this can help if you have pretty low
S/N data). On line 4, we let
for a first attempt at a fit (this can help if you have pretty low
S/N data). On line 4, we let 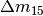 go free. On line 5,
we specify more rest-band filters. On line 6 we add more filters to
the fit and allow the host extinction to vary, though keeping
go free. On line 5,
we specify more rest-band filters. On line 6 we add more filters to
the fit and allow the host extinction to vary, though keeping
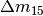 and
and 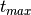 fixed at the values determined from the previous fit
(all fitted parameters and their errors are saved as member data of
the
fixed at the values determined from the previous fit
(all fitted parameters and their errors are saved as member data of
the sn instance). On line 7, we allow all parameters to vary.
On line 8, we save the fit to a file that can be later loaded into
SNooPy (using something like s=load(filename)).
Unless you specify otherwise, all the fitting is done
in flux units (SNooPy takes care of converting magnitudes to fluxes,
if needed, for both the observations and models). Note that because
the LMA is an non-linear least-squares solving
routine, it is not guaranteed to find the global minimum 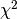 .
It is your responsibility to inspect the fit to make sure it got it
right.
.
It is your responsibility to inspect the fit to make sure it got it
right.
Getting the Results¶
After the fit has run, the best-fit value of each parameter can be
retrieved as member variables of the sn class. The uncertainty
in the parameter have the same name, but with e_ prepended. You
can also run the sn.summary() function to print out a summary of
the fit. The full covariance matrix is also available as a dictionary.
To get 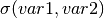 , simply refer to
, simply refer to
sn.model.C['var1']['var2'].
The Meaning of the Uncertainties¶
The errors reported by the fitting are simply statistical errors. They are determined in the usual least-squares way of inverting the Hesssian of the model at the location of the best-fit. The errors therefore reflect how constrained the parameters are by the data.
It is important to keep in mind that the entire light-curve is used to
constrain the parameters. So for example, the time of B-band maximum, Tmax
may have a very small uncertainty compared to what you get by fitting a
polynomial to the observed data near maximum. The same holds true for the
fit value of 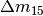 versus a direct measurement from a
spline of the observed B-band data.
versus a direct measurement from a
spline of the observed B-band data.
Each model has a function systematics that you can call once the fit is
complete. This will report additional systmatic errors that may be in the
model. For example:
In[1]: s.choose_model('EBV_model')
In[2]: s.fit()
In[3]: s.model.systmatics()
Out[6]: {'DM': 0.2276, 'EBVhost': 0.06, 'Tmax': None, 'dm15': None}
The systmatics in the distance modulus include the intrinsic dispersion of the Phillips relation and the uncertainty in the calibration parameters from [Folatelli+2010].
Examples¶
To load a SN and fit all filters with the default EBV_model:
In[1]: s = get_sn('somefile.txt')
In[2]: s.fit()
To change to the color_model and fit using the color-stretch as
a light-curve parameter, holding Rv fixed:
In[3]: s.choose_model('color_model', stype='st')
In[4]: s.fit(Rv=2.1)
Fit all filters with max_model, using the color-stretch. Then, fit each
filter independently, keeping the color-stretch and k-corrections
from the previous fit. Store results in a dictionary:
In[5]: s.choose_model('max_model', stype='st')
In[6]: s.fit()
In[7]: maxs = {}; e_maxs = {}; Tmaxs = {}
In[8]: for filt in s.data:
...: s.fit([filt], st=s.st, kcorr=False, reset_kcorrs=False)
...: Tmaxs[filt], maxs[filt], e_maxs[filt],f = s.get_max(filt, deredden=True)
| [Prieto+2006] | Prieto et al., ApJ, 647, 501 (2006) http://adsabs.harvard.edu/abs/2006ApJ...647..501P |
| [Folatelli+2010] | Folatelli et al., AJ, 139, 120 (2010). http://adsabs.harvard.edu/abs/2010AJ....139..120F |