SIGMA (σ) IMAGE AND CHI² (χ²) FAQ

The sigma image (σ_x,y) and χ_ν² are two things that may need some explanation for new users of GALFIT. Both things are defined in the traditional way as found in standard literature on statistics. The concept is important to understand for getting sensible fit results, for interpreting when a fit is acceptable, and for interpreting the relative merits of different fits. Most optimization algorithms use χ_ν² statistics to figure out how to converge on a better solution, or, once a solution has converged, what is the statistical significance of the fit. GALFIT is no different from a simple line or curve fitting algorithm when it comes to computing χ_ν² statistics. Therefore, everything you learned about from excellent books on statistics such as "Data Reduction and Error Analysis" by Bevington & Robinson, or "An Introduction to Error Analysis" by Taylor is applicable in GALFIT in a straightforward manner. So, this section is not intended to be a thorough introduction to basic statistics. Instead, I will try to make some abstractions more concrete for beginners of statistics, and to show how the abstractions are implemented in practice. If there are issues that need clarification below, users are very much welcome to contact me.

A question that often comes up when fitting a line to data points, or a function to imaging data, is: "why do you need to know the sigma at each data point at all?" The answer is that it's the only way for a computer to know when a fit is "good enough." But what does "good enough" mean, really? You might say that "good enough" is when a function runs through all the data points "as closely as possible." But, one then might ask, "are all the points equally good, or are some better than others?" Even if the data are perfect -- no cosmic ray hits, no dead/hot pixels, no flatfielding problems -- uncertainty from counting statistics alone means that all points are not equal. What does that mean exactly? It means that in an image, pixels that have high signal are also generally more certain, relatively speaking, compared to pixels that have fewer counts. So our intuition tells us that we don't want our fit to be equally weighted by uncertain data points in the same way as more certain ones. On the other hand, our intuition also says that the more pixels we have in an area, the more certain we are also about the the average flux value in that area, even if the fluxes there are small. This tells us that you'll want to include the number of pixels when considering an overall uncertainty, such that the "effective uncertainty" should go down with the number of data points that you have. In nature, the scheme for what we just described is Poisson statistics, where the weights are precisely Gaussian σ weights. Once you come to terms with this then the use of the sigma image becomes clear: it is a map of how uncertain the flux is at every pixel.

The sigma map is used directly in calculating the χ_ν² quantity. In words, χ_ν² is simply a sum of deviations between the data flux and the best fitting model, relative to expected deviation (σ) at each pixel, the whole thing squared. And the form of the equation looks like:

In the above equation N_dof is the number of degrees of freedom in the fit, which is roughly N_dof ~ nx × ny. The definition is approximate because usually the number of free parameters in the fit is subtracted from nx × ny in the definition of N_dof, but that number is generally quite small compared to the number of pixels, and is thus often not so important. GALFIT computes χ_ν² and uses the definition of sigma in the standard way: in the equation above, f_data(x,y) is your data at pixel (x,y) and f_model(x,y) is a value that GALFIT generates at pixel (x,y), and σ(x,y) on the denominator is the Poisson (Gaussian) deviate of the flux at (x,y). In other words, σ(x,y) is what is known in GALFIT as the "sigma image" where σ sometimes corresponds to the standard deviation of the flux at that pixel. 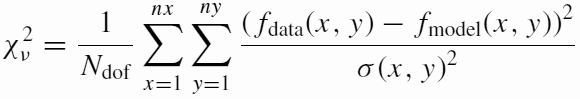Just to be compact, I will use the forms data_x,y, model_x,y, and σ_x,y for the three terms, instead of carrying around the f and the parentheses. In a hand-wavy sense, if your model is a perfect fit to your data, each pixel will have difference (data_x,y - model_x,y), the term on the numerator, that is roughly the size of σ_x,y, on the denominator. So given the quantity in the summation is close to one, and you sum it up N_dof time (where N_dof = nx × ny is the number of pixels), then divided by N_dof, it's no surprise χ_ν² should be close to 1 if a fit is perfect. That's why when you have an appropriate model, and you get a good fit, the rule of thumb is that χ_ν² is, in principle, on the order of unity. This is only a rule of thumb because... imagine the following situation where every pixel (sky in an image) except for one (the object you're interested in) is fit well. If the number of pixels is large, χ_ν² will be close to one. Nevertheless, it's still a bad fit because you're not interested in the sky, which is dominating the statistics, and the object (the one pixel) is fit poorly by the model. A second useful rule of thumb to get an idea whether a sigma image is half-way reasonable or just totally wrong is to simply fit the SKY with a sky function in GALFIT, whence χ_ν² should come out close to unity (if the noise is not correlated). This is a good **sanity check**, but it doesn't guarantee that the sigma image is right. The third thing that should be said about the equation above is that the sigma image needs to have the same units as your data image: if your flux (numerator) is in units of counts/second, but your sigma image (denominator) is in units of counts, then your χ_ν² is off by factors of (exposure time²). If your χ_ν²'s appears really really low, this is most likely the reason why.

Side-bar: You will often hear people say that the above equation is based on the Gaussian noise model. The "Gaussian" reference is with regard to σ_x,y, because σ_x,y is the dispersion centered around the mean flux μ of a Gaussian function ~exp[-(f-μ)²/2σ²]. What this means is that if you can repeat observations an infinite number of times and record all the outcome, you'd be able to pin-point μ perfectly, and each individual measurement scatters around μ in a Gaussian distributed way -- meaning 68% of the time each flux measurement will be within ± σ of the mean μ, and 32% of the time the deviation is larger than σ from the mean μ value. Because this hypothetical Gaussian distribution is not something you can observe (you'd have to make an infinite number of observations), you can't observe σ_x,y directly. What we can do is to *infer* σ_x,y from our data -- and the more counts you have (i.e. S/N), the closer is your estimate of σ from the truth. We can blindly estimate σ_x,y at each pixel often without too much fuss, because σ_x,y can be easily estimated from Poisson statistics, going roughly like the √pixel value. What is much more of a problem in galaxy fitting is the assumption that flux_x,y scatters around the mean (model_x,y) like σ -- this is patently not true most of the time because our models aren't perfect, either because there's a profile mismatch, the galaxies aren't perfect ellipses, we can't fit every single blob in an image, the PSF is imperfect -- there are numerous other reasons. In other words, the residuals are not due to only Poisson noise, but mostly due to structures we can't subtract away perfectly. So the assumption of Gaussianity is why, in galaxy fitting, χ² doesn't mean very much. Because the rigorous meaning of the χ² analysis is violated to a large extent, the error bar on parameters which come out of the analysis, don't mean much either, except perhaps in low signal-to-noise situations when the noise dominates over non-Poisson fluctuations.

The saving grace for why the analysis is still meaningful, despite major violation of statistical principles, are two facts: first, in astronomy we are mostly interested in relative comparisons rather than an absolute measurement of each object for its own sake. Secondly, in response to signal-to-noise (i.e. exposure time), the scatter of the parameters around their mean value behaves like random noise (see Barden et al. 2008, ApJS, 175, 105), rather than in some unpredictable way. This latter fact does not have to be true: the model fit could in principle be dominated by the fluctuations on top of the galaxy profile which comes and goes with S/N. Therefore, it is still important to get the sigma image right because it controls the relative weights between the bright and faint pixels in the fit. If you get the sigma image really wrong, it will not be easy to interpret the profile parameters such as the Sérsic index n, for example, or to compare one object to another.

Now that we have the formalities out of the way, we can address the most frequently asked questions:

• How does GALFIT calculate the sigma image?: If you don't provide your own sigma image, GALFIT will generate one internally to estimate χ². There is really only ONE correct way to calculate the sigma image, and infinite ways to get it wrong. To know what's the right way and what's the wrong way, you have to know what has been done to your data. By this I mean: have your data been averaged or summed from multiple images? Has the image been divided by the exposure time? Has any other scaling factor been applied to it?

  In any case, if you want to construct your own sigma image, or have GALFIT generate a correct image, you have to be able to answer the questions posed above before reading further. If you want to know what has been done to your data, the person to ask would be the one who took and reduced your data. It is nearly impossible for anyone else to tell, just by looking at a data, what has been done to it.

  Because there is only one way to get the correct sigma image, if you want GALFIT to create one internally, you have to give it an image that has the format it knows how to deal with, and not one that has some funky units. The format GALFIT expects is where the ADUs are in counts (not counts/second), where GAIN is used to convert counts from ADUs into electrons via the operation GAIN × ADU, and where the data image is obtained by averaging over N images (and that info is in the image header where NCOMBINE = N). Are these things true for your data?

  Based on GAIN, and NCOMBINE of the data you feed into GALFIT, it converts all the pixel values first into electrons, does the noise calculation, then converts everything back to the same units as the input data. The reason you want to convert pixel values into electrons is that Poisson statistics apply to electrons. It's not that you can't account for the scaling some other way, but GALFIT only knows one way. Equivalently, instead of converting things into electrons then back again, one can "propagate the errors" by keeping track of all the scaling terms and change the GAIN parameter, if you know what I'm driving at (if not, forget it). So that is all the basic idea. If you want to create your own sigma image, you have to perform similar operations.

  If you give GALFIT an image in the format it expects, then the conversion from ADUs into the sigma image is the following:

  1. GALFIT converts pixel ADUs into electrons by doing: ADU × GAIN × NCOMBINE using parameters found in the image header.
  2. GALFIT adds the result with the RMS of the sky in quadrature (and RMS is multiplied by √NCOMBINE).
  3. GALFIT takes √image from step 2, and divides it by the GAIN, thereby converting electrons back into ADUs. This is now the sigma image.

  There is an underlying assumption in this process, which is that the sky dominates the image region being fitted, so that the RMS of the sky can be estimated directly from that region. If the object dominates the fitting region the sigma image GALFIT estimates will not be accurate.

• If I used MULTIDRIZZLE to put together my HST images, how do I make a sigma image from outputs of the data pipeline?: MULTIDRIZZLE (Casertano et al. 2000, AJ, 120: 2747) produces an useful by-product that has an image extension "wht" when the parameter "final_wht_type" is set to "ERR." It keeps track of error sources during the reduction process that GALFIT would otherwise know nothing about (see Casertano et al. 2000 for details). The ".wht" image is directly related to the sigma image that can be fed into GALFIT. But, currently it is not clear to me how doing so affects the image quality in the final image combination. The user is well advised to find out directly from the MULTIDRIZZLE documentation and from experimenting rather than to take this FAQ for granted.

• What do I need to do to create my own sigma image?: The simplest explanation is that you need to convert your image ADUs into electrons first. To do that, you have to know what has been done to your data. Once you converted your ADUs to electrons, then sum the Poisson uncertainty at each pixel with the other noise sources in quadrature (e.g. detector readnoise). After you do so, convert the electrons back into ADUs by reversing the first step.

• Why is the χ_ν² value so low?: To calculate χ_ν², GALFIT needs to know about the sigma (i.e. square root of the variance, a.k.a. noise) at each pixel. If it isn't provided in Parameter C, GALFIT will generate one internally based on exposure time, readnoise, gain, and ncombine image header parameters (please see "When one doesn't have an input noise image" in the section on Advisory on using GALFIT). What's often the case is that the image pixels have units of counts/second, instead of counts. When this happens, GALFIT will not know how to convert pixel values into Poisson noise, and the χ_ν² will be very low. If you provide a sigma image that has the same units as the data image, GALFIT won't care what the units are. However, the exposure time must always be consistent with the image pixel values, or else the total magnitude will be incorrect.

Now that you think you have to get the sigma image perfectly, the fact is that one only has to get the sigma image roughly right because the fits turn out not to be super sensitive to the sigma map. To the extent that the actual value of χ² in galaxy fitting is mostly meaningless (because the residuals will mostly not be Gaussian distributed about the mean), except in relative terms, getting the normalization wrong, by messing up the GAIN or NCOMBINE values, is a bad habit that should be actively discouraged, but it doesn't affect how the parameters come out in the fit. It is more important to get the pedestal right, which is another reason for why the fitting region has to be fairly large compared to the galaxy. The fact that the fit is not too sensitive to the sigma image is a really good thing, because often times we don't know it all that well for various reasons. This fact should ease one's mind a little, but not so much that it stops one from trying to get the most accurate sigma map. If the sigma map is wrong, we really don't know our data, and there certainly are situations where getting it right is crucial to the science. Often, wrong sigma images will be most noticeable for galaxies with low S/N but may sometimes show up for even high S/N objects (see here).

Go back to GALFIT Home Page.
Go back to Chien Peng's Home Page.

Chien Peng ()