

GALFIT 3.0 (Peng et al. 2010, AJ, 139, 2097) tries to address some of issues raised above in new and flexible ways, while retaining the most useful traditional qualitative sense of galaxy fitting. What makes parametric fitting highly useful traditionally are the fact that we can easily intuit what the fits mean when they are described by analytic functions (e.g. Sérsic, Nuker, Gaussian, etc.), and the profile parameters can be easily compared against other galaxies in a statistical fashion. Therefore, a key requirement in devising a more flexible scheme is to retain those key elements even when things deviate greatly from an ellipse, e.g. the meaning of the concentration index should not change when a profile is lopsided. GALFIT 3.0 now allows even more diverse shapes than previously possible in 2-D, and is able to fit a wide range of isophotal shapes, axial twists, and spiral structures of many spiral galaxies. All the while, the radial profile parameters of each component can be thought of in the traditional way, no matter how complex they may get.
How GALFIT accomplishes the intended objectives is to use the concept of Fourier modes and coordinate rotation functions, which are two different ideas. When first hearing about Fourier modes, a natural tendency is to think about ``shapelet'' or ``wavelet'' decomposition. However, it is important to realize that GALFIT does not do shapelet, wavelet, or even Fourier decomposition on an image in pixel space. Delving into this a little bit, the idea of shapelets/wavelets analysis is very much analogous to Fourier transforming an image into an infinite series sum of basis functions. But instead of Sines and Cosines as the bases, they use more complicated mathematical patterns called shapelets or wavelets (for the purpose of reducing the number of terms needed to characterize an object). Because orthogonality is required to make a mathematical transform unique, those basis functions often do not look like the object or components that one is modeling. The shapelet/wavelet technique is not a ``fit'' in the sense of galaxy fitting (although some iteration might be required to find the center of a galaxy); shapelets/wavelets are a mathematical inversion of an image just like Fourier transform. In the limit of infinite shapelets/wavelets, one can model everything in an image, down to the noise. The basis functions, and their linear combination, often do not have a straight forward association with identifiable physical subcomponents. Whether this is a benefit or not depends on what you want to do (as is true with all techniques). This is the principle difference between shapelet/wavelet analysis and 2-D parametric fitting: in 2-D parametric fitting, the GALFIT model components are themselves priors about the presence of bars, disks, bulges, nuclear star clusters, an AGN, or what not.
In GALFIT3.0 the radial profile parameters still mean exactly the same as what we used to understand. The only difference is that the azimuthal shape can be more complicated than a simple ellipse. Although more abstract, this is not that unusual of an idea since the venerable ellipse used in traditional 2-D fitting (i.e. GALFIT prior to 3.0) is itself modified from a perfect circle using the axis ratio parameter, q. The novelty is that instead of a closed analytic form, the shape can be thought of as a series expansion, with the most useful terms being the lowest order ones. Also, the terms are very meaningful and intuitive once one gets used to the idea. In fact, the ellipsoid axis ratio term is really just a special case of Fourier modes (i.e. mostly the second mode). The motivation for going to higher modes is to model the radial profile and shape of each component as accurately as possible, as though each *might* represent some kind of physical reality (e.g. bulge, disk, spiral, AGN, rings). This makes the components easier to interpret, in contrast to the shapelet basis functions described above. In a single component fit, the model takes on a shape that is flux weighted average over all the radii, minimizing residuals in the least-squares sense.
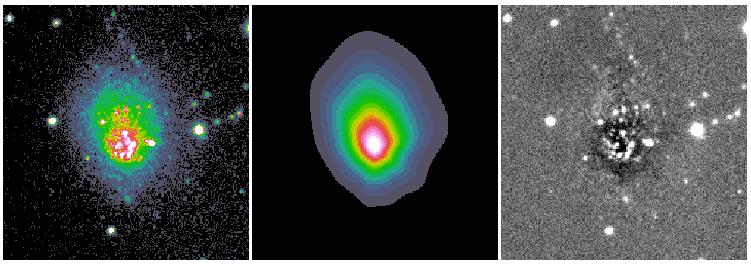
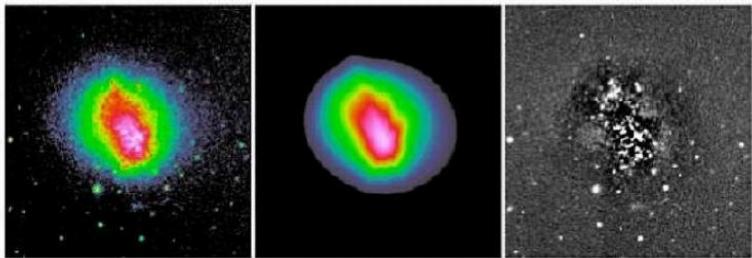
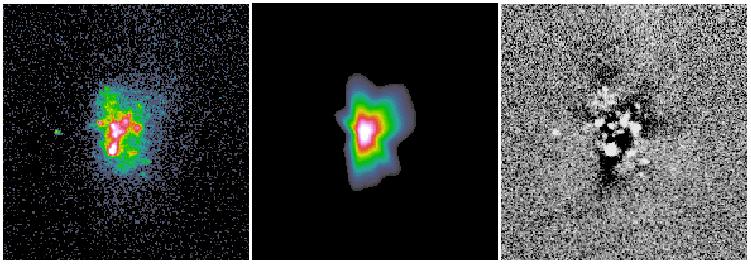
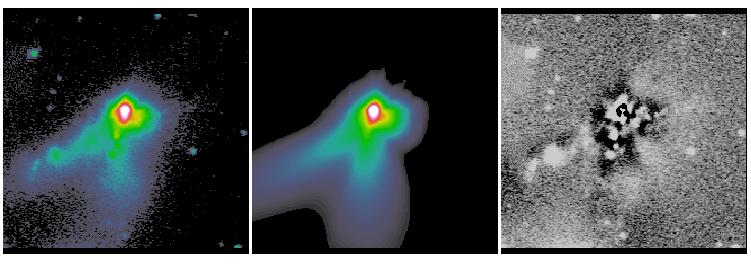
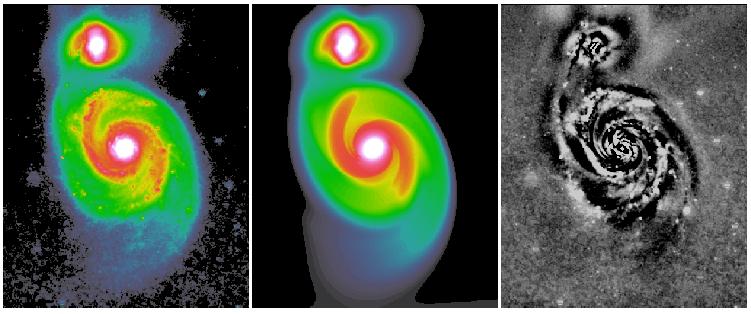
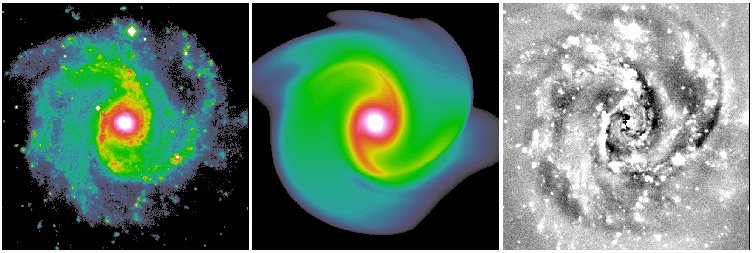
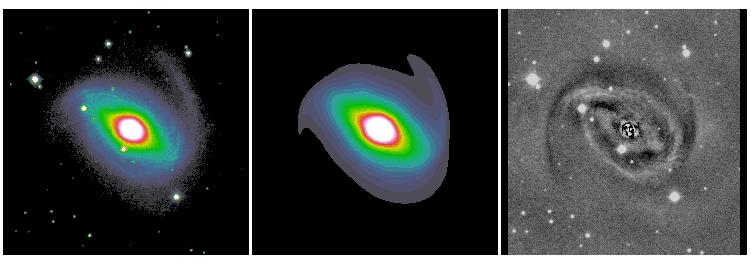
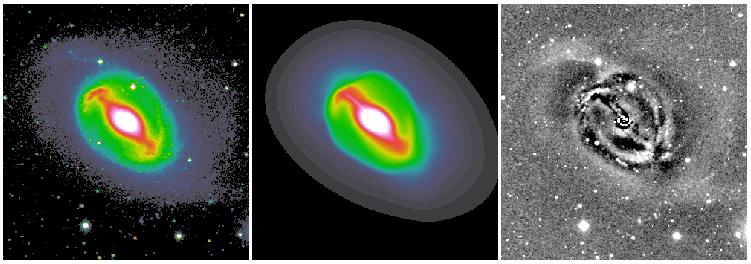
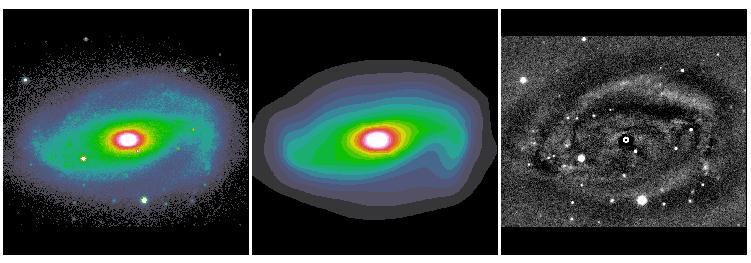
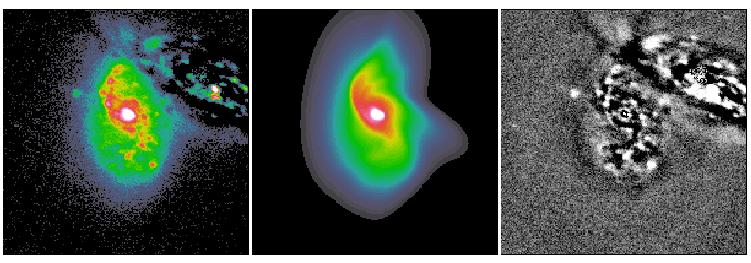
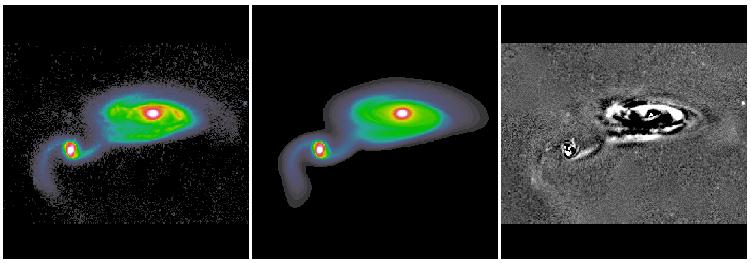
The other new idea deals with isophotal twists and spiral structures. Most objects have some sort of isophotal twists, even elliptical galaxies. In spiral galaxies isophotal twists are mostly attributed to spiral arms. What most people do in galaxy bulge-to-disk decomposition is to sweep the large residuals from spiral structures under-the-rug. This is fine in some cases, and may not be in others. In elliptical galaxies isophotal twists may not necessary mean there are two distinct physical components. This is often a problem for really nearby galaxies but not so much at z > 0.3 or so, because isophotal twist happens mostly toward the center and can't be resolved when galaxies are too far away to be resolved clearly. To deal with isophotal twists, GALFIT uses a coordinate rotation technique to rotate the isophotes as a function of radius. For details, see here. Below are some examples that show show the idea does seem to work.
Both the Fourier and coordinate rotation techniques will be described in detail in Peng et al. 2010 (AJ, 139, 2097). Below are some examples of the new techniques applied to real galaxies. All the images were provided to me to analyze by colleagues whose names are listed below.













 )
)